题目内容
6.某种黄金饰品在甲、乙两个商店销售,甲店标价280元/克,按标价出售,不优惠,乙店标价300元/克,但若买的黄金饰品重量超过3克,则超出部分可打八折出售.(1)分另写出到甲、乙商店购买该种黄金饰品所需费用y(元)和重量x(克)之间的函数关系,并写出定义域;
(2)李阿姨要买一条重量不超过10克的此种黄金饰品,到哪个商店购买最合算?请说明理由.
分析 (1))根据等量关系“去甲商店购买所需费用=标价×重量”“去乙商店购买所需费用=标价×3+标价×0.8×超出3克的重量(x>3);当x≤3时,y乙=530x,”列出函数关系式;
(2)通过比较甲乙两商店费用的大小,得到购买一定重量的黄金饰品去最合算的商店.
解答 解:(1)到甲商店购买所需费用y和重量x之间的函数关系为:y甲=280x,(x≥0),
到乙商店购买所需费用y和重量x之间的函数关系:
当0≤x≤3时,y乙=300x,
当x>3时,y乙=300×3+300×0.8×(x-3)=240x+180;
(2)当0<x≤3时,显然y甲<y乙,故此时到甲商店购买合算;
①当y甲=y乙时,即:280x=240x+180,解得:x=4.5,
∴当x=4.5时,到甲、乙两商店购买一样;
②当y甲<y乙时,即:280x<240x+180,解得:x<4.5,
∴当x<4.5时,到甲商店购买合算;
③当y甲>y乙时,即:280x>240x+180,解得:x>4.5,
∴当x>4.5时,到乙商店购买合算;
综上,当0<x<4.5时,到甲商店购买合算;当x=4.5时,到两商店购买一样合算;当4.5<x≤10时,到乙商店购买合算.
点评 此题考查了一次函数与一元一次不等式的应用,关键是读懂题意,列出函数关系式和不等式,再根据实际情况进行讨论,不要漏解.

练习册系列答案
相关题目
14.下列说法正确的是( )
| A. | (3,2)和(2,3)表示一个点 | B. | 点($\sqrt{3}$,0)在x轴的正半轴上 | ||
| C. | 点(-2,4)在第四象限 | D. | 点(3,-1)到x轴的距离为3 |
15.±$\sqrt{(-16)^{2}}$的值是( )
| A. | ±16 | B. | ±4 | C. | 16 | D. | -16 |

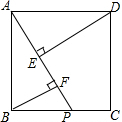 如图,正方形ABCD中,点P在BC边上,DE⊥AP于点E,BF⊥AP于点F,若BF=x,DE=y,EF=2,求y与x的函数关系式,并画出函数图象.
如图,正方形ABCD中,点P在BC边上,DE⊥AP于点E,BF⊥AP于点F,若BF=x,DE=y,EF=2,求y与x的函数关系式,并画出函数图象.