题目内容
17.如图所示,AB∥CD,分别写出下面四个图形中∠A与∠P、∠C的关系,请你从所得到的关系中任选一图的结论加以证明.
分析 ①过点P作PE∥AB,利用平行线的性质,易得∠APC=∠1+∠2=∠PAB+∠PCD;
②过点P作PE∥AB,利用平行线的性质,易得∠PAB=∠APC+∠1=∠APC+∠PAD;
③延长BA交PC于点E,利用平行线与三角形外角的性质,可求得答案;
④利用平行线与三角形外角的性质,可求得答案.
解答 解:①如图(1)中,结论:∠APC=∠PAB+∠PCD,
理由:过点P作PE∥AB,
∵AB∥CD,
∴PE∥AB∥CD,
∴∠1=∠PAB,∠2=∠PCD,
∴∠APC=∠1+∠2=∠PAB+∠PCD;
②如图(2)中,结论:∠PAB+∠APC+∠PCD=360°.
理由:过点P作PE∥AB,
∵AB∥CD,
∴PE∥AB∥CD,
∴∠1+∠PAB=180°,∠2+∠PCD=180°,
∴∠PAB+∠APC+∠PCD=360°;
③如图(3)中,∠PAB=∠APC+∠PCD.
结论:延长BA,交PC于点E,
∵AB∥CD,
∴∠1=∠PCD,
∴∠PAB=∠APC+∠1=∠APC+∠PAD;
④如图(4)中,结论:∠PCD=∠PAB+∠APC,
理由:∵AB∥CD,
∴∠1=∠PCD,
∴∠PCD=∠1=∠APC+∠PCD;
点评 此题考查了平行线的性质以及三角形外角的性质,学会添加辅助线的方法,解题的关键是灵活应用三角形外角、平行线性质,此题难度适中,属于中考常考题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,在△ABC中,BD是中线,且BD=$\frac{1}{2}$AC,求证:∠ABC=90°.
如图,在△ABC中,BD是中线,且BD=$\frac{1}{2}$AC,求证:∠ABC=90°.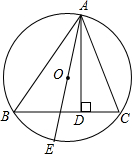 如图,△ABC是⊙O的内接三角形,AD⊥BC于点D,AE是⊙O的直径,若S△ABC=S,⊙O的半径为R.求证:
如图,△ABC是⊙O的内接三角形,AD⊥BC于点D,AE是⊙O的直径,若S△ABC=S,⊙O的半径为R.求证: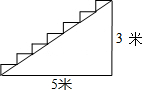 如图一楼梯宽2m,现要在表面铺地毯,而地毯每平米需要30元,那么购买地毯至少需要480元.
如图一楼梯宽2m,现要在表面铺地毯,而地毯每平米需要30元,那么购买地毯至少需要480元.