题目内容
14.已知分式方程x+$\frac{10x-{x}^{2}}{x-5}$=-5的解是a,求当y为何值时,分式$\frac{2a}{y-1}$比分式$\frac{y-6}{1-y}$大4?分析 求出已知分式方程的解确定出a的值,根据题意列出分式方程,求出解,即可作出判断.
解答 解:解分式方程x+$\frac{10x-{x}^{2}}{x-5}$=-5,得x=$\frac{5}{2}$,
经检验,得x=$\frac{5}{2}$是分式方程的解,即a=$\frac{5}{2}$,
由题意可得$\frac{5}{y-1}$-$\frac{y-6}{1-y}$=4,
解得:y=1,
经检验,得y=1不是分式方程的解,即不存在满足条件的y值,使得$\frac{2a}{y-1}$比$\frac{y-6}{1-y}$大4.
点评 此题考查了解分式方程,熟练掌握运算法则是解本题的关键.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案 53天天练系列答案
53天天练系列答案
相关题目
19.下列说法中,正确是( )
| A. | 对角线相等的四边形是矩形 | |
| B. | 一组对边平行,另一组对边相等的四边形是平行四边形 | |
| C. | 对角线互相垂直平分的四边形是菱形 | |
| D. | 一组邻边相等,并且有一个内角为直角的四边形是正方形 |
3.已知函数:y=$\frac{4}{x}$(x>0),下列对此函数描述正确的是( )
| A. | 该函数关于原点对轴 | B. | 该图象存在于第三象限 | ||
| C. | 该图象有一条对称轴 | D. | 该图象过点(1,-4) |
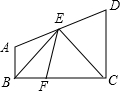 如图,四边形ABCD中,AB∥DC,E是AD上一点,且BE平分∠ABC,CE平分∠BCD,在BC上取一点F,使BF=AB
如图,四边形ABCD中,AB∥DC,E是AD上一点,且BE平分∠ABC,CE平分∠BCD,在BC上取一点F,使BF=AB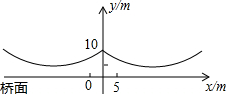 如图所示,桥梁的两条钢缆具有相同的抛物线形状,按照图中的直角坐标系,右面的一条抛物线可以用y=0.0225x2+0.9x+10 表示,而且左、右两条抛物线关于y轴对称.
如图所示,桥梁的两条钢缆具有相同的抛物线形状,按照图中的直角坐标系,右面的一条抛物线可以用y=0.0225x2+0.9x+10 表示,而且左、右两条抛物线关于y轴对称.