题目内容
3.甲、乙两名队员参加射击训练,成绩分别被制成下列两个统计图:
根据以上信息,整理分析数据如下:
| 平均成绩/环 | 中位数/环 | 众数/环 | 方差 | |
| 甲 | a | 7 | 7 | 1.2 |
| 乙 | 7 | b | 8 | c |
(2)分别运用表中的四个统计量,简要分析这两名队员的射击训练成绩.若选派其中一名参赛,你认为应选哪名队员?
分析 (1)利用平均数的计算公式直接计算平均分即可;将乙的成绩从小到大重新排列,用中位数的定义直接写出中位数即可;根据乙的平均数利用方差的公式计算即可;
(2)结合平均数和中位数、众数、方差三方面的特点进行分析.
解答 解:(1)甲的平均成绩a=$\frac{5×1+6×2+7×4+8×2+9×1}{1+2+4+2+1}$=7(环),
∵乙射击的成绩从小到大重新排列为:3、4、6、7、7、8、8、8、9、10,
∴乙射击成绩的中位数b=$\frac{7+8}{2}$=7.5(环),
其方差c=$\frac{1}{10}$×[(3-7)2+(4-7)2+(6-7)2+2×(7-7)2+3×(8-7)2+(9-7)2+(10-7)2]
=$\frac{1}{10}$×(16+9+1+3+4+9)
=4.2;
(2)从平均成绩看甲、乙二人的成绩相等均为7环,从中位数看甲射中7环以上的次数小于乙,从众数看甲射中7环的次数最多而乙射中8环的次数最多,从方差看甲的成绩比乙的成绩稳定;
综合以上各因素,若选派一名队员参加比赛的话,可选择乙参赛,因为乙获得高分的可能更大.
点评 本题考查的是条形统计图和方差、平均数、中位数、众数的综合运用.熟练掌握平均数的计算,理解方差的概念,能够根据计算的数据进行综合分析.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
13.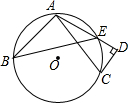 如图,点A,B,C是⊙O上三点,AD和过C点的切线互相垂直,垂足为D,AD交⊙O于点E,若CD=3,AC=5,则cos∠ABE的值为( )
如图,点A,B,C是⊙O上三点,AD和过C点的切线互相垂直,垂足为D,AD交⊙O于点E,若CD=3,AC=5,则cos∠ABE的值为( )
 如图,点A,B,C是⊙O上三点,AD和过C点的切线互相垂直,垂足为D,AD交⊙O于点E,若CD=3,AC=5,则cos∠ABE的值为( )
如图,点A,B,C是⊙O上三点,AD和过C点的切线互相垂直,垂足为D,AD交⊙O于点E,若CD=3,AC=5,则cos∠ABE的值为( )| A. | $\frac{7}{12}$ | B. | $\frac{7}{24}$ | C. | $\frac{24}{25}$ | D. | $\frac{16}{25}$ |
14.已知等边三角形的边长为3,点P为等边三角形内任意一点,则点P到三边的距离之和为( )
| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{3\sqrt{3}}{2}$ | C. | $\frac{3}{2}$ | D. | 不能确定 |
11.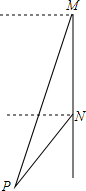 如图,轮船沿正南方向以30海里/时的速度匀速航行,在M处观测到灯塔P在西偏南68°方向上,航行2小时后到达N处,观测灯塔P在西偏南46°方向上,若该船继续向南航行至离灯塔最近位置,则此时轮船离灯塔的距离约为(由科学计算器得到sin68°=0.9272,sin46°=0.7193,sin22°=0.3746,sin44°=0.6947)( )
如图,轮船沿正南方向以30海里/时的速度匀速航行,在M处观测到灯塔P在西偏南68°方向上,航行2小时后到达N处,观测灯塔P在西偏南46°方向上,若该船继续向南航行至离灯塔最近位置,则此时轮船离灯塔的距离约为(由科学计算器得到sin68°=0.9272,sin46°=0.7193,sin22°=0.3746,sin44°=0.6947)( )
 如图,轮船沿正南方向以30海里/时的速度匀速航行,在M处观测到灯塔P在西偏南68°方向上,航行2小时后到达N处,观测灯塔P在西偏南46°方向上,若该船继续向南航行至离灯塔最近位置,则此时轮船离灯塔的距离约为(由科学计算器得到sin68°=0.9272,sin46°=0.7193,sin22°=0.3746,sin44°=0.6947)( )
如图,轮船沿正南方向以30海里/时的速度匀速航行,在M处观测到灯塔P在西偏南68°方向上,航行2小时后到达N处,观测灯塔P在西偏南46°方向上,若该船继续向南航行至离灯塔最近位置,则此时轮船离灯塔的距离约为(由科学计算器得到sin68°=0.9272,sin46°=0.7193,sin22°=0.3746,sin44°=0.6947)( )| A. | 22.48 | B. | 41.68 | C. | 43.16 | D. | 55.63 |
18. 如图,一扇形纸扇完全打开后,外侧两竹条AB和AC的夹角为120°,AB长为25cm,贴纸部分的宽BD为15cm,若纸扇两面贴纸,则贴纸的面积为( )
如图,一扇形纸扇完全打开后,外侧两竹条AB和AC的夹角为120°,AB长为25cm,贴纸部分的宽BD为15cm,若纸扇两面贴纸,则贴纸的面积为( )
 如图,一扇形纸扇完全打开后,外侧两竹条AB和AC的夹角为120°,AB长为25cm,贴纸部分的宽BD为15cm,若纸扇两面贴纸,则贴纸的面积为( )
如图,一扇形纸扇完全打开后,外侧两竹条AB和AC的夹角为120°,AB长为25cm,贴纸部分的宽BD为15cm,若纸扇两面贴纸,则贴纸的面积为( )| A. | 175πcm2 | B. | 350πcm2 | C. | $\frac{800}{3}$πcm2 | D. | 150πcm2 |
8.二次函数y=2x2-3的图象是一条抛物线,下列关于该抛物线的说法,正确的是( )
| A. | 抛物线开口向下 | B. | 抛物线经过点(2,3) | ||
| C. | 抛物线的对称轴是直线x=1 | D. | 抛物线与x轴有两个交点 |
15. 如图,一个放置在水平桌面上的圆柱,它的主(正)视图是( )
如图,一个放置在水平桌面上的圆柱,它的主(正)视图是( )
 如图,一个放置在水平桌面上的圆柱,它的主(正)视图是( )
如图,一个放置在水平桌面上的圆柱,它的主(正)视图是( )| A. |  | B. |  | C. |  | D. |  |
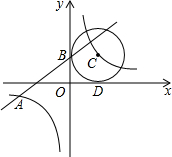 如图,已知一次函数y1=kx+b的图象与反比例函数y2=$\frac{4}{x}$的图象交于点A(-4,m),且与y轴交于点B,第一象限内点C在反比例函数y2=$\frac{4}{x}$的图象上,且以点C为圆心的圆与x轴,y轴分别相切于点D,B
如图,已知一次函数y1=kx+b的图象与反比例函数y2=$\frac{4}{x}$的图象交于点A(-4,m),且与y轴交于点B,第一象限内点C在反比例函数y2=$\frac{4}{x}$的图象上,且以点C为圆心的圆与x轴,y轴分别相切于点D,B 已知不等式组$\left\{\begin{array}{l}{x≥-a-1}&{①}\\{-x≥-b}&{②}\end{array}\right.$,在同一条数轴上表示不等式①,②的解集如图所示,则b-a的值为$\frac{1}{3}$.
已知不等式组$\left\{\begin{array}{l}{x≥-a-1}&{①}\\{-x≥-b}&{②}\end{array}\right.$,在同一条数轴上表示不等式①,②的解集如图所示,则b-a的值为$\frac{1}{3}$.