题目内容
12.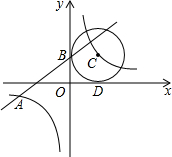 如图,已知一次函数y1=kx+b的图象与反比例函数y2=$\frac{4}{x}$的图象交于点A(-4,m),且与y轴交于点B,第一象限内点C在反比例函数y2=$\frac{4}{x}$的图象上,且以点C为圆心的圆与x轴,y轴分别相切于点D,B
如图,已知一次函数y1=kx+b的图象与反比例函数y2=$\frac{4}{x}$的图象交于点A(-4,m),且与y轴交于点B,第一象限内点C在反比例函数y2=$\frac{4}{x}$的图象上,且以点C为圆心的圆与x轴,y轴分别相切于点D,B(1)求m的值;
(2)求一次函数的表达式;
(3)根据图象,当y1<y2<0时,写出x的取值范围.
分析 (1)直接将A点代入反比例函数解析式求出答案;
(2)直接利用切线的性质结合正方形的判定与性质得出C,B点坐标,进而利用待定系数法求出一次函数解析式;
(3)利用A点坐标结合函数图象得出x的取值范围.
解答 解:(1)把点A(-4,m)的坐标代入y2=$\frac{4}{x}$,
则m=$\frac{4}{-4}$=-1,
得m=-1;
(2)连接CB,CD, ∵⊙C与x轴,y轴相切于点D,B,
∵⊙C与x轴,y轴相切于点D,B,
∴∠CBO=∠CDO=90°=∠BOD,BC=CD,
∴四边形BODC是正方形,
∴BO=OD=DC=CB,
∴设C(a,a)代入y2=$\frac{4}{x}$得:a2=4,
∵a>0,∴a=2,
∴C(2,2),B(0,2),
把A(-4,-1)和(0,2)的坐标代入y1=kx+b中,
得:$\left\{\begin{array}{l}{-4k+b=-1}\\{b=2}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=\frac{3}{4}}\\{b=2}\end{array}\right.$,
∴一次函数的表达式为:y1=$\frac{3}{4}$x+2;
(3)∵A(-4,-1),
∴当y1<y2<0时,x的取值范围是:x<-4.
点评 此题主要考查了反比例函数与一次函数的交点,正确求出C,B点坐标是解题关键.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目
3.甲、乙两名队员参加射击训练,成绩分别被制成下列两个统计图:

根据以上信息,整理分析数据如下:
(1)写出表格中a,b,c的值;
(2)分别运用表中的四个统计量,简要分析这两名队员的射击训练成绩.若选派其中一名参赛,你认为应选哪名队员?

根据以上信息,整理分析数据如下:
| 平均成绩/环 | 中位数/环 | 众数/环 | 方差 | |
| 甲 | a | 7 | 7 | 1.2 |
| 乙 | 7 | b | 8 | c |
(2)分别运用表中的四个统计量,简要分析这两名队员的射击训练成绩.若选派其中一名参赛,你认为应选哪名队员?
4.下列计算正确的是( )
| A. | $\sqrt{12}$=2$\sqrt{3}$ | B. | $\sqrt{\frac{3}{2}}$=$\frac{\sqrt{3}}{2}$ | C. | $\sqrt{-{x}^{3}}$=x$\sqrt{-x}$ | D. | $\sqrt{{x}^{2}}$=x |
1.某校九年级共有1、2、3、4四个班,现从这四个班中随机抽取两个班进行一场篮球比赛,则恰好抽到1班和2班的概率是( )
| A. | $\frac{1}{8}$ | B. | $\frac{1}{6}$ | C. | $\frac{3}{8}$ | D. | $\frac{1}{2}$ |




 如图,直线a∥b,∠1=45°,∠2=30°,则∠P=75°.
如图,直线a∥b,∠1=45°,∠2=30°,则∠P=75°.