题目内容
8.二次函数y=2x2-3的图象是一条抛物线,下列关于该抛物线的说法,正确的是( )| A. | 抛物线开口向下 | B. | 抛物线经过点(2,3) | ||
| C. | 抛物线的对称轴是直线x=1 | D. | 抛物线与x轴有两个交点 |
分析 根据二次函数的性质对A、C进行判断;根据二次函数图象上点的坐标特征对B进行判断;利用方程2x2-3=0解的情况对D进行判断.
解答 解:A、a=2,则抛物线y=2x2-3的开口向上,所以A选项错误;
B、当x=2时,y=2×4-3=5,则抛物线不经过点(2,3),所以B选项错误;
C、抛物线的对称轴为直线x=0,所以C选项错误;
D、当y=0时,2x2-3=0,此方程有两个不相等的实数解,所以D选项正确.
故选D.
点评 本题考查了二次函数的性质:对于二次函数y=ax2+bx+c(a≠0),它的顶点坐标是(-$\frac{b}{2a}$,$\frac{4ac-{b}^{2}}{4a}$),对称轴为直线x=-$\frac{b}{2a}$,二次函数y=ax2+bx+c(a≠0)的图象具有如下性质:当a>0时,抛物线y=ax2+bx+c(a≠0)的开口向上,x<-$\frac{b}{2a}$时,y随x的增大而减小;x>-$\frac{b}{2a}$时,y随x的增大而增大;当a<0时,抛物线y=ax2+bx+c(a≠0)的开口向下,x<-$\frac{b}{2a}$时,y随x的增大而增大;x>-$\frac{b}{2a}$时,y随x的增大而减小.

练习册系列答案
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案
相关题目
18.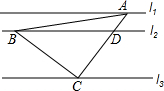 如图,直线l1∥l2∥l3,一等腰直角三角形ABC的三个顶点A,B,C分别在l1,l2,l3上,∠ACB=90°,AC交l2于点D,已知l1与l2的距离为1,l2与l3的距离为3,则$\frac{AB}{BD}$的值为( )
如图,直线l1∥l2∥l3,一等腰直角三角形ABC的三个顶点A,B,C分别在l1,l2,l3上,∠ACB=90°,AC交l2于点D,已知l1与l2的距离为1,l2与l3的距离为3,则$\frac{AB}{BD}$的值为( )
 如图,直线l1∥l2∥l3,一等腰直角三角形ABC的三个顶点A,B,C分别在l1,l2,l3上,∠ACB=90°,AC交l2于点D,已知l1与l2的距离为1,l2与l3的距离为3,则$\frac{AB}{BD}$的值为( )
如图,直线l1∥l2∥l3,一等腰直角三角形ABC的三个顶点A,B,C分别在l1,l2,l3上,∠ACB=90°,AC交l2于点D,已知l1与l2的距离为1,l2与l3的距离为3,则$\frac{AB}{BD}$的值为( )| A. | $\frac{4\sqrt{2}}{5}$ | B. | $\frac{\sqrt{34}}{5}$ | C. | $\frac{5\sqrt{2}}{8}$ | D. | $\frac{20\sqrt{2}}{23}$ |
19.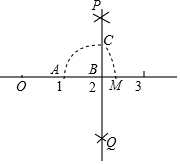 如图,数轴上点A,B分别对应1,2,过点B作PQ⊥AB,以点B为圆心,AB长为半径画弧,交PQ于点C,以原点O为圆心,OC长为半径画弧,交数轴于点M,则点M对应的数是( )
如图,数轴上点A,B分别对应1,2,过点B作PQ⊥AB,以点B为圆心,AB长为半径画弧,交PQ于点C,以原点O为圆心,OC长为半径画弧,交数轴于点M,则点M对应的数是( )
 如图,数轴上点A,B分别对应1,2,过点B作PQ⊥AB,以点B为圆心,AB长为半径画弧,交PQ于点C,以原点O为圆心,OC长为半径画弧,交数轴于点M,则点M对应的数是( )
如图,数轴上点A,B分别对应1,2,过点B作PQ⊥AB,以点B为圆心,AB长为半径画弧,交PQ于点C,以原点O为圆心,OC长为半径画弧,交数轴于点M,则点M对应的数是( )| A. | $\sqrt{3}$ | B. | $\sqrt{5}$ | C. | $\sqrt{6}$ | D. | $\sqrt{7}$ |
16.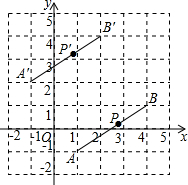 如图,线段AB经过平移得到线段A′B′,其中点A,B的对应点分别为点A′,B′,这四个点都在格点上.若线段AB上有一个点P( a,b),则点P在A′B′上的对应点P′的坐标为( )
如图,线段AB经过平移得到线段A′B′,其中点A,B的对应点分别为点A′,B′,这四个点都在格点上.若线段AB上有一个点P( a,b),则点P在A′B′上的对应点P′的坐标为( )
 如图,线段AB经过平移得到线段A′B′,其中点A,B的对应点分别为点A′,B′,这四个点都在格点上.若线段AB上有一个点P( a,b),则点P在A′B′上的对应点P′的坐标为( )
如图,线段AB经过平移得到线段A′B′,其中点A,B的对应点分别为点A′,B′,这四个点都在格点上.若线段AB上有一个点P( a,b),则点P在A′B′上的对应点P′的坐标为( )| A. | (a-2,b+3) | B. | (a-2,b-3) | C. | (a+2,b+3) | D. | (a+2,b-3) |
3.甲、乙两名队员参加射击训练,成绩分别被制成下列两个统计图:

根据以上信息,整理分析数据如下:
(1)写出表格中a,b,c的值;
(2)分别运用表中的四个统计量,简要分析这两名队员的射击训练成绩.若选派其中一名参赛,你认为应选哪名队员?

根据以上信息,整理分析数据如下:
| 平均成绩/环 | 中位数/环 | 众数/环 | 方差 | |
| 甲 | a | 7 | 7 | 1.2 |
| 乙 | 7 | b | 8 | c |
(2)分别运用表中的四个统计量,简要分析这两名队员的射击训练成绩.若选派其中一名参赛,你认为应选哪名队员?
18.数据4,8,4,6,3的众数和平均数分别是( )
| A. | 5,4 | B. | 8,5 | C. | 6,5 | D. | 4,5 |
 如图,△ABC内接于⊙O,AH⊥BC于点H,若AC=24,AH=18,⊙O的半径OC=13,则AB=$\frac{39}{2}$.
如图,△ABC内接于⊙O,AH⊥BC于点H,若AC=24,AH=18,⊙O的半径OC=13,则AB=$\frac{39}{2}$.



 如图,直线a∥b,∠1=45°,∠2=30°,则∠P=75°.
如图,直线a∥b,∠1=45°,∠2=30°,则∠P=75°.