题目内容
14. 如图,以半圆的半径8为直径在半圆内作一个圆,求图中阴影部分的面积.
如图,以半圆的半径8为直径在半圆内作一个圆,求图中阴影部分的面积.
分析 由题意可知:阴影部分的面积=半圆的面积-小圆的面积,半圆的半径等于小圆的直径,半圆的直径已知,从而可以分别求出半圆和小圆的面积,进而求出阴影部分的面积.
解答 解:因为半圆的半径=16÷2=8,
小圆的半径=8÷2=4,
且${S_{半圆}}=\frac{1}{2}•π•{8^2}=32π$,
${S_圆}=π•{4^2}=16π$,
所以S阴=S半圆-S圆,
=32π-16π,
=16π,
=16×3.14,
=50.24(平方单位);
答:阴影部分的面积是50.24平方单位.
点评 此题主要考查圆的面积的计算方法,关键是明白:半圆的半径等于小圆的直径.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
4.在正整数中,1是( )
| A. | 最小的奇数 | B. | 最小的偶数 | C. | 最小的素数 | D. | 最小的合数 |
9.若a+b=0,则a与b之间的关系是( )
| A. | 相等 | B. | 互为倒数 | ||
| C. | 互为相反数 | D. | 一个是正数一个是负数 |
3.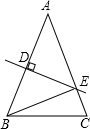 已知:如图,在△ABC中,AB=AC,DE是AB的垂直平分线,若BE+CE=12,BC=8,则△ABC的周长为( )
已知:如图,在△ABC中,AB=AC,DE是AB的垂直平分线,若BE+CE=12,BC=8,则△ABC的周长为( )
 已知:如图,在△ABC中,AB=AC,DE是AB的垂直平分线,若BE+CE=12,BC=8,则△ABC的周长为( )
已知:如图,在△ABC中,AB=AC,DE是AB的垂直平分线,若BE+CE=12,BC=8,则△ABC的周长为( )| A. | 20 | B. | 32 | C. | 24 | D. | 36 |