题目内容
17.四边形ABCD的对角线AC、BD相交于点O.下列条件中,能判断四边形ABCD是平行四边形的是( )| A. | AD=BC,AB∥CD | B. | AO=CO,AD=BC | C. | AD∥BC,∠ADC=∠ABC | D. | AD=BC,∠ABD=∠CDB |
分析 根据平行四边形的判定方法即可判断.
解答 解:A、错误.四边形ABCD可能是等腰梯形.
B、错误.不满足是平行四边形的条件.
C、正确.由AD∥BC,∠ADC=∠ABC,可以推出△ABD≌△CDB,得到AB=CD,所以四边形ABCD是平行四边形.
D、错误.四边形ABCD可能是等腰梯形.
故选C.
点评 本题考查平行四边形的判断、解题的关键是记住平行四边形的判定方法:两组对边分别平行的四边形是平行四边形.两组对边分别相等的四边形是平行四边形.
一组对边平行且相等的四边形是平行四边形.两组对角分别相等的四边形是平行四边形.对角线互相平分的四边形是平行四边形.属于中考常考题型.

练习册系列答案
相关题目
7.在△ABC中,∠C=90°,∠A=30°,若CD是高,且CD=1,则a,b,c三边的长分别是( )
| A. | a=$\sqrt{3}$,b=2,c=$\sqrt{7}$ | B. | a=2,b=$\frac{2\sqrt{3}}{3}$,c=$\frac{4\sqrt{3}}{3}$ | C. | a=$\frac{2\sqrt{3}}{3}$,b=2,c=$\frac{4\sqrt{3}}{3}$ | D. | a=2,b=2,c=4 |
8.解方程组$\left\{\begin{array}{l}{ax+by=2}\\{cx-7y=8}\end{array}\right.$时,某同学把c看错后得到$\left\{\begin{array}{l}{x=-2}\\{y=2}\end{array}\right.$,而正确的解是$\left\{\begin{array}{l}{x=3}\\{y=-2}\end{array}\right.$,那么a、b、c的值是( )
| A. | a=4,b=5,c=2 | B. | a,b,c的值不能确定 | ||
| C. | a=4,b=5,c=-2 | D. | a,b不能确定,c=-2 |
2.若关于x,y的二元一次方程组$\left\{\begin{array}{l}{2x+y=3k-1}\\{x+2y=2k+3}\end{array}\right.$的解满足x-y<0,则k的取值范围是( )
| A. | k>2 | B. | k<2 | C. | k>4 | D. | k<4 |
6.已知一次函数y=(b-9)x+b+4的图象经过第一、二、四象限,则b的值不可能为( )
| A. | -3 | B. | 0 | C. | 7 | D. | 12 |
7.2016年4月30日至5月2日,河北省共接待游客1708.3万人次,实现旅游收入106.5亿元,旅行社的小王想了解某企业员工个人的旅游年消费情况,他随机抽取部分员工进行调查,并将统计结果绘制成如表所示的频数分布表,则下列说法中不正确的是( )
| 个人旅游年消费金额x/元 | x≤2000 | 2000<x≤4000 | 4000<x≤6000 | 6000<x≤8000 | 8000<x≤10000 |
| 频数 | 12 | 25 | 31 | 22 | 10 |
| A. | 小王随机抽取了100名员工 | |
| B. | 在频数分布表中,组距是2000,组数是5组 | |
| C. | 个人旅游年消费金额在6000元以上的人数占随机抽取人数的22% | |
| D. | 在随机抽取的员工中,个人旅游年消费金额在4000元以下的共有37人 |
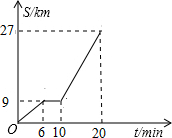 如图所示是鼎龙高速路口开往宁都方向的某汽车行驶的路程s(km)与时间t(分钟)的函数关系图,观察图中所提供的信息,解答下列问题:
如图所示是鼎龙高速路口开往宁都方向的某汽车行驶的路程s(km)与时间t(分钟)的函数关系图,观察图中所提供的信息,解答下列问题: 如图,在平行四边形ABCD中,AB=$\sqrt{29}$,AD=4,将平行四边形ABCD沿AE翻折后,点B恰好与点C重合,则折痕AE的长为( )
如图,在平行四边形ABCD中,AB=$\sqrt{29}$,AD=4,将平行四边形ABCD沿AE翻折后,点B恰好与点C重合,则折痕AE的长为( )