题目内容
已知⊙O的半径为5,AB、AC是⊙O内的两条弦,且AB=5
,AC=5
,求∠BAC的度数.
| 2 |
| 3 |
考点:垂径定理,特殊角的三角函数值
专题:分类讨论
分析:根据题意点C的位置有两种情况,如图1,∠BAC=∠CAO+∠OAB;如图2,∠BAC=∠OAB-∠OAC,进而得出答案.
解答: 解:如图1,连接OC,OA,OB,过点O作OE⊥AC于点E,
解:如图1,连接OC,OA,OB,过点O作OE⊥AC于点E,
∵OA=OB=5,AB=5
,
52+52=(5
)2,
∴∠AOB=90°,
∴△OAB是等腰直角三角形,∠OAB=45°,
∵AC=5
,OE⊥AC,
∴AE=
,
∴cos∠EAO=
=
,
∴∠EAO=30°,
∴如图1时,∠BAC=∠CAO+∠OAB=30°+45°=75°;
如图2时,∠BAC=∠BAC=∠OAB-∠OAC.=45°-30°=15°.
 解:如图1,连接OC,OA,OB,过点O作OE⊥AC于点E,
解:如图1,连接OC,OA,OB,过点O作OE⊥AC于点E,∵OA=OB=5,AB=5
| 2 |
52+52=(5
| 2 |
∴∠AOB=90°,
∴△OAB是等腰直角三角形,∠OAB=45°,
∵AC=5
| 3 |
∴AE=
5
| ||
| 2 |
∴cos∠EAO=
| ||||
| 5 |
| ||
| 2 |
∴∠EAO=30°,
∴如图1时,∠BAC=∠CAO+∠OAB=30°+45°=75°;
如图2时,∠BAC=∠BAC=∠OAB-∠OAC.=45°-30°=15°.
点评:此题主要考查了垂径定理以及勾股定理逆定理,利用分类讨论得出是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列数轴的画法中正确的是( )
A、 |
B、 |
C、 |
D、 |
 如图,已知△ABC的∠ABC和∠ACB的角平分线交于P,∠A=50°,则∠P=
如图,已知△ABC的∠ABC和∠ACB的角平分线交于P,∠A=50°,则∠P=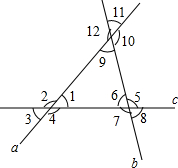 如图所示,a、b两条直线交于一点,生成∠9,探索∠9与原有角的位置关系.
如图所示,a、b两条直线交于一点,生成∠9,探索∠9与原有角的位置关系. 如图,边长为5的菱形ABCD中,AE⊥BC于点E,且AE=4.以AE为边向右作正方形AEFG.边GF与CD交于点H.
如图,边长为5的菱形ABCD中,AE⊥BC于点E,且AE=4.以AE为边向右作正方形AEFG.边GF与CD交于点H.