题目内容
 如图,已知△ABC的∠ABC和∠ACB的角平分线交于P,∠A=50°,则∠P=
如图,已知△ABC的∠ABC和∠ACB的角平分线交于P,∠A=50°,则∠P=考点:三角形内角和定理
专题:
分析:根据三角形内角和定理求出∠ABC+∠ACB=180°-∠A=130°,根据角平分线定义得出∠PBC=
∠ABC,∠PCB=
∠ACB,求出∠PBC+∠PCB=65°,代入∠P=180°-(∠PBC+∠PCB)求出即可.
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:∵∠A=50°,
∴∠ABC+∠ACB=180°-∠A=130°,
∵∠ABC和∠ACB的角平分线交于P,
∴∠PBC=
∠ABC,∠PCB=
∠ACB,
∴∠PBC+∠PCB=
×130°=65°,
∴∠P=180°-(∠PBC+∠PCB)=115°,
故答案为:115°.
∴∠ABC+∠ACB=180°-∠A=130°,
∵∠ABC和∠ACB的角平分线交于P,
∴∠PBC=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠PBC+∠PCB=
| 1 |
| 2 |
∴∠P=180°-(∠PBC+∠PCB)=115°,
故答案为:115°.
点评:本题考查了三角形的内角和定理和角平分线定义的应用,注意:三角形的内角和等于180°,题目比较好,难度适中.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
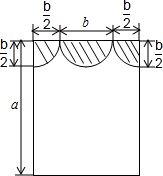 如图,小红家装饰新家,小红为自己的房间选择了一款窗帘,请你帮她计算:
如图,小红家装饰新家,小红为自己的房间选择了一款窗帘,请你帮她计算: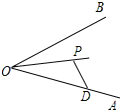 如图,已知点P为∠AOB的角平分线上的一点,点D在边OA上.爱动脑筋的小刚经过仔细观察后,进行如下操作:在边OB上取一点E,使得PE=PD,如果∠ODP=35°,则∠OEP的度数为
如图,已知点P为∠AOB的角平分线上的一点,点D在边OA上.爱动脑筋的小刚经过仔细观察后,进行如下操作:在边OB上取一点E,使得PE=PD,如果∠ODP=35°,则∠OEP的度数为 已知,在⊙O中,
已知,在⊙O中,
 如图,等边△ABC的3个顶点都在⊙O上,请把这个图形补成一个中心对称图形.
如图,等边△ABC的3个顶点都在⊙O上,请把这个图形补成一个中心对称图形. 如图,菱形ABCD的对角线AC、BD相交于点O,且AC=24,BD=10,过点O作OH丄AB,垂足为H,则点O到边AB的距离
如图,菱形ABCD的对角线AC、BD相交于点O,且AC=24,BD=10,过点O作OH丄AB,垂足为H,则点O到边AB的距离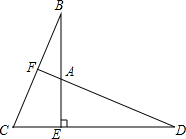 已知:BE⊥CD,BE=DE,EC=EA.求证:△BEC≌△DEA.
已知:BE⊥CD,BE=DE,EC=EA.求证:△BEC≌△DEA.