题目内容
在△ABC中,已知∠ABC=45°,BD⊥AC于D,CD=2,AD=3,则BD的长为 .
考点:正方形的判定与性质,全等三角形的判定与性质,勾股定理,旋转的性质
专题:
分析:由题意可得出△ABD≌△ABE,△CBD≌△CBF,推出∠DBA=∠EBA,∠DBC=∠FBC,求出四边形BEGF是正方形,设BD=x,则BE=EG=GF=x,AG=x-3,CG=x-2,在Rt△,AGC中根据勾股定理求出(x-3)2+(x-2)2=(2+3)2,求出即可.
解答:解: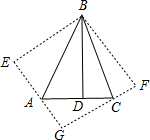
分别以BA和BC为对称轴在△ABC的外部作△BDA和△BDC的对称图形△BEA和△BFC,如图,
由题意可得:△ABD≌△ABE,△CBD≌△CBF
∴∠DBA=∠EBA,∠DBC=∠FBC,
又∵∠ABC=45°
∴∠EBF=90°,
又∵AD⊥BC,
∴∠E=∠ADB=90°,∠F=∠BDC=90°,
又∵BE=BD,BF=BD,
∴BE=BF,
∴四边形BEGF是正方形,
设BD=x,则BE=EG=GF=x,
∵CD=2,AD=3,
∴BE=2,CF=3
∴AG=x-3,CG=x-2,
在Rt△,AGC中,AG2+CG2=AC2,
(x-3)2+(x-2)2=(2+3)2,
x1=6,x2=-1(舍去),
即BD=6,
故答案为:6.

分别以BA和BC为对称轴在△ABC的外部作△BDA和△BDC的对称图形△BEA和△BFC,如图,
由题意可得:△ABD≌△ABE,△CBD≌△CBF
∴∠DBA=∠EBA,∠DBC=∠FBC,
又∵∠ABC=45°
∴∠EBF=90°,
又∵AD⊥BC,
∴∠E=∠ADB=90°,∠F=∠BDC=90°,
又∵BE=BD,BF=BD,
∴BE=BF,
∴四边形BEGF是正方形,
设BD=x,则BE=EG=GF=x,
∵CD=2,AD=3,
∴BE=2,CF=3
∴AG=x-3,CG=x-2,
在Rt△,AGC中,AG2+CG2=AC2,
(x-3)2+(x-2)2=(2+3)2,
x1=6,x2=-1(舍去),
即BD=6,
故答案为:6.
点评:本题考查了正方形的性质和判定,旋转的性质,全等三角形的性质和判定,勾股定理的应用,题目比较好,综合性比较强,难度偏大.

练习册系列答案
相关题目
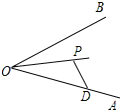 如图,已知点P为∠AOB的角平分线上的一点,点D在边OA上.爱动脑筋的小刚经过仔细观察后,进行如下操作:在边OB上取一点E,使得PE=PD,如果∠ODP=35°,则∠OEP的度数为
如图,已知点P为∠AOB的角平分线上的一点,点D在边OA上.爱动脑筋的小刚经过仔细观察后,进行如下操作:在边OB上取一点E,使得PE=PD,如果∠ODP=35°,则∠OEP的度数为
 已知,在⊙O中,
已知,在⊙O中,
 如图,等边△ABC的3个顶点都在⊙O上,请把这个图形补成一个中心对称图形.
如图,等边△ABC的3个顶点都在⊙O上,请把这个图形补成一个中心对称图形.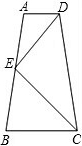 如图,梯形ABCD中,AD∥BC,E为AB中点,且AD+BC=DC,求证:DE⊥EC,DE平分∠ADC,CE平分∠BCD.
如图,梯形ABCD中,AD∥BC,E为AB中点,且AD+BC=DC,求证:DE⊥EC,DE平分∠ADC,CE平分∠BCD.