题目内容
8.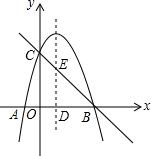 如图,抛物线y=-x2+bx+c交x轴于点B(3,0),交y轴交于点C(0,3),抛物线的对称轴交x轴于点D.
如图,抛物线y=-x2+bx+c交x轴于点B(3,0),交y轴交于点C(0,3),抛物线的对称轴交x轴于点D.(1)求抛物线的解析式;
(2)点F是直线BC上方的抛物线上的一个动点,过点F作y轴的平行线交直线BC于点E,当点F运动到什么位置时,线段EF的长度最大?求线段EF长度的最大值.
分析 (1)将点B,点C的坐标代入函数的解析式,得到关于b、c的方程组,然后解得b、c的值即可;
(2)先求得直线BC的解析式,设点F的横坐标为x,然后求得可求得点E与点F的纵坐标,从而得到EF的函数关系式,最后利用配方法求得EF的最值以及点F的坐标即可.
解答 解:(1)把B(3,0)C(0,3)代入y=-x2+bx+c得
$\left\{\begin{array}{l}{-9+3b+c=0}\\{c=3}\end{array}\right.$,
解得$\left\{\begin{array}{l}{b=2}\\{c=3}\end{array}\right.$,
故抛物线的解析式为y=-x2+2x+3;
(2)设直线BC的解析式为y=kx+b,将点B、C的坐标代入得:$\left\{\begin{array}{l}{3k+b=0}\\{b=3}\end{array}\right.$
解得:$\left\{\begin{array}{l}{k=-1}\\{b=3}\end{array}\right.$.
∴直线BC的解析式为y=-x+3.
设点F的坐标为(x,-x2+2x+3),点E的坐标为(x,-x+3).
∴EF=-x2+2x+3-(-x+3)=-x2+3x=-(x-$\frac{3}{2}$)2+$\frac{9}{4}$.
∴当x=$\frac{3}{2}$时,点F的坐标为($\frac{3}{2}$,$\frac{15}{4}$),EF的最大值为$\frac{9}{4}$.
点评 本题主要考查的是二次函数的图象和性质,利用配方法求得EF的最大值是解题的关键.

练习册系列答案
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
16.在a,b,c,d,e中有3个负数,则abcde的积( )
| A. | 大于0 | B. | 小于0 | C. | 大于或等于0 | D. | 小于或等于0 |
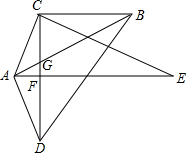 在Rt△ACE中,CF⊥AE于F,延长CF于D,使CF=FD,连结AD,G为CF上一点,连结AG并延长至B,连结BD和BC,使∠CBA=∠ABD=∠E.
在Rt△ACE中,CF⊥AE于F,延长CF于D,使CF=FD,连结AD,G为CF上一点,连结AG并延长至B,连结BD和BC,使∠CBA=∠ABD=∠E.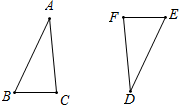 如图,△ABC和△DEF关于点O成心对称.
如图,△ABC和△DEF关于点O成心对称.
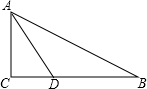 如图,在△ABC中,∠C=90°,∠B=30°,BC=6cm,AD是∠CAB的平分线,求DC的长.
如图,在△ABC中,∠C=90°,∠B=30°,BC=6cm,AD是∠CAB的平分线,求DC的长.