题目内容
6.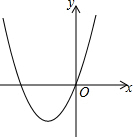 已知抛物线的顶点为(-2,-3),且经过原点,
已知抛物线的顶点为(-2,-3),且经过原点,(1)求抛物线的解析式;
(2)求该抛物线与x轴的交点;
(3)直接写出当y<0时,x的取值范围.
分析 (1)由抛物线的对称性可知然后利用待定系数法求解即可;
(2)利用抛物线的对称性可求得与x轴的另一个交点坐标为(-4,0);
(3)根据函数图形确定出x的取值范围即可.
解答 解:(1)∵抛物线的顶点为(-2,-3),且经过原点,
∴抛物线经过点(-4,0).
设抛物线的解析式为y=ax(x+4),将x=-2,y=-3代入得:-4a=-3,
解得:a=$\frac{3}{4}$.
∴抛物线的解析式为y=$\frac{3}{4}$x2+3x.
(2)∵抛物线的顶点为(-2,-3),且经过原点,
∴抛物线经过点(-4,0).
∴抛物线与x轴交点的坐标为(-4,0)、(0,0).
(3)由函数图形可知当-4<x<0时,y<0,
∴x的取值范围是-4<x<0.
点评 本题主要考查的是二次函数的图象和性质,掌握二次函数的图象和性质是解题的关键.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案
相关题目
16.在a,b,c,d,e中有3个负数,则abcde的积( )
| A. | 大于0 | B. | 小于0 | C. | 大于或等于0 | D. | 小于或等于0 |
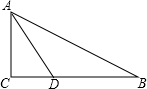 如图,在△ABC中,∠C=90°,∠B=30°,BC=6cm,AD是∠CAB的平分线,求DC的长.
如图,在△ABC中,∠C=90°,∠B=30°,BC=6cm,AD是∠CAB的平分线,求DC的长.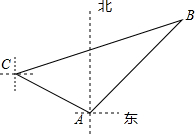 如图,我国海上休渔结束后,甲、乙两艘捕鱼船分别从相距30$\sqrt{2}$千米的A港、C港出海捕鱼,C港在A港北偏西60°处,甲船以每小时15千米的速度沿东北方向航行,甲船航行2小时后乙船快速(匀速)沿北偏东75°的方向航行,结果两船在B处相遇.
如图,我国海上休渔结束后,甲、乙两艘捕鱼船分别从相距30$\sqrt{2}$千米的A港、C港出海捕鱼,C港在A港北偏西60°处,甲船以每小时15千米的速度沿东北方向航行,甲船航行2小时后乙船快速(匀速)沿北偏东75°的方向航行,结果两船在B处相遇.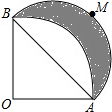 如图,AB=2cm,∠AOB=90°,OA=OB,以OA为半径作$\widehat{AB}$,以AB为半径作半圆$\widehat{AMB}$,则$\widehat{AMB}$和$\widehat{AB}$所围成的阴影部分面积为1cm2.
如图,AB=2cm,∠AOB=90°,OA=OB,以OA为半径作$\widehat{AB}$,以AB为半径作半圆$\widehat{AMB}$,则$\widehat{AMB}$和$\widehat{AB}$所围成的阴影部分面积为1cm2.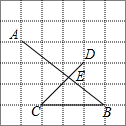 如图,网格图中每个方格都是边长为1的正方形,点A,B,C,D是格点,若线段AB交CD于点E,则线段AE的长是$\frac{20}{7}$.
如图,网格图中每个方格都是边长为1的正方形,点A,B,C,D是格点,若线段AB交CD于点E,则线段AE的长是$\frac{20}{7}$.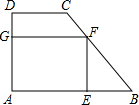 如图,在梯形ABCD中,AB∥CD,∠A=90°,AB=7,CD=4,AD=2,在梯形中作一个矩形AEFG,使E在AB上,F在BC上,G在AD上.
如图,在梯形ABCD中,AB∥CD,∠A=90°,AB=7,CD=4,AD=2,在梯形中作一个矩形AEFG,使E在AB上,F在BC上,G在AD上.