题目内容
如图由13个相同的正方形构成,若在标明字母的点之间连上线段,则(∠FPB+∠APC+∠APD+∠APE)+(∠EQA+∠FQ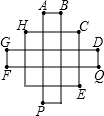 H+∠FQC+∠GQA)=( )
H+∠FQC+∠GQA)=( )
 H+∠FQC+∠GQA)=( )
H+∠FQC+∠GQA)=( )| A、540° | B、450° |
| C、405° | D、360° |
考点:正方形的性质,余角和补角
专题:
分析:根据正方形的性质和余角的定义,将所求各角巧妙地进行组合即可求解.
解答:解:∵∠APC+∠APE=90°,∠FPB+∠APD=90°+∠APB,∠EQA=90°,∠FQH+∠FQC=90°,∠GQA=45°-∠APB,
∴(∠FPB+∠APC+∠APD+∠APE)+(∠EQA+∠FQH+∠FQC+∠GQA)
=90°+90°+∠APB+90°+90°+45°-∠APB
=405°.
故选C.

∴(∠FPB+∠APC+∠APD+∠APE)+(∠EQA+∠FQH+∠FQC+∠GQA)
=90°+90°+∠APB+90°+90°+45°-∠APB
=405°.
故选C.
点评:考查了正方形的性质和余角的定义,得到∠APC+∠APE=90°,∠FPB+∠APD=90°+∠APB,∠EQA=90°,∠FQH+∠FQC=90°,∠GQA=45°-∠APB是解题的关键.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
同时满足x:(x+y+1)=2y:(x+2y+3)和(3x+2y-xy):(x+5y-2xy)=1:2的x,y为( )
A、x=
| ||||
B、x=-
| ||||
| C、x=7,y=35 | ||||
| D、x=1,y=5 |
有一枚牌子,正面是1,反面是0,则将牌子连续丢两次,则两次的数字之和为1的概率是( )
A、
| ||
B、
| ||
C、
| ||
| D、1 |
已知△ABC的三条长a、b、c满足b+c=8,bc=a2-12a+52,则△ABC的形状一定是( )
| A、等腰三角形 |
| B、直角三角形 |
| C、等腰直角三角形 |
| D、无法确定 |
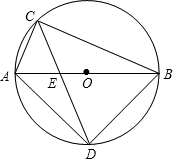 ⊙O中,AB为直径,CD平分∠ACB交⊙O于D,求证:
⊙O中,AB为直径,CD平分∠ACB交⊙O于D,求证: