题目内容
若a，b，c满足a+b+c=a5+b5+c5=0，则a3+b3+c3= ．
考点：立方公式
专题：
分析：首先根据a5+b5+c5-abc（2a2+2b2+2c2+3）=（a+b+c）（a4+b4+c4-ab3-ac3-a3b-a3c-a3b-bc3）和题干条件a+b+c=a5+b5+c5=0，求出abc=0，然后根据a3+b3+c3-3abc=（a+b+c）（a2+b2+c2-ab-bc-ac）即可求出a3+b3+c3的值．
解答：解：a5+b5+c5-abc（2a2+2b2+2c2+3）
=（a+b+c）（a4+b4+c4-ab3-ac3-a3b-a3c-a3b-bc3）
又知a+b+c=a5+b5+c5=0，
即abc=0，
又知a3+b3+c3-3abc=（a+b+c）（a2+b2+c2-ab-bc-ac）=0，
故a3+b3+c3=0．
故答案为0．
=（a+b+c）（a4+b4+c4-ab3-ac3-a3b-a3c-a3b-bc3）
又知a+b+c=a5+b5+c5=0，
即abc=0，
又知a3+b3+c3-3abc=（a+b+c）（a2+b2+c2-ab-bc-ac）=0，
故a3+b3+c3=0．
故答案为0．
点评：本题主要考查立方根的知识点，解答本题的突破口是根据a+b+c=0，a5+b5+c5=0求得abc=0，本题难度不大．
练习册系列答案
优百分课时互动系列答案
开心蛙状元作业系列答案
课时掌控随堂练习系列答案
相关题目
已知x3+y3-z3=96，xyz=4，x2+y2+z2-xy+xz+yz=12，则x+y-z=（ ）
| A、6 | B、7 | C、8 | D、9 |
如图由13个相同的正方形构成，若在标明字母的点之间连上线段，则（∠FPB+∠APC+∠APD+∠APE）+（∠EQA+∠FQ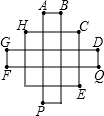
H+∠FQC+∠GQA）=（ ）
H+∠FQC+∠GQA）=（ ）| A、540° | B、450° |
| C、405° | D、360° |
设
=
，则(
+
) ÷
=（ ）
| b |
| a+b |
| a-b |
| 3a-b |
| 2a2+b2 |
| 2a2-b2 |
| a2-8b2 |
| a2+8b2 |
| 2a |
| 3b |
A、
| ||
B、-
| ||
C、-
| ||
D、
|