题目内容
已知△ABC的三条长a、b、c满足b+c=8，bc=a2-12a+52，则△ABC的形状一定是（ ）
| A、等腰三角形 |
| B、直角三角形 |
| C、等腰直角三角形 |
| D、无法确定 |
考点：因式分解的应用
专题：计算题
分析：先根据b+c=8可得b=8-c①，再把①代入bc=a2-12a+52中，并进行配方运算，可得（a-6）2+（c-4）2=0，
结合非负数的性质易求a、c，进而可求b，再利用勾股定理的逆定理易判断此三角形不是直角三角形，从而可知此三角形是等腰三角形．
结合非负数的性质易求a、c，进而可求b，再利用勾股定理的逆定理易判断此三角形不是直角三角形，从而可知此三角形是等腰三角形．
解答：解：由b+c=8可得
b=8-c①，
把①代入bc=a2-12a+52中得
a2-12a+52+c2-8c=0，
即a2-12a+36+c2-8c+16=0，
那么（a-6）2+（c-4）2=0，
∴a=6，c=4，
且b=4，
∴b=c=4，a=6，
又∵42+42≠62，
∴△ABC是等腰三角形．
故选A．
b=8-c①，
把①代入bc=a2-12a+52中得
a2-12a+52+c2-8c=0，
即a2-12a+36+c2-8c+16=0，
那么（a-6）2+（c-4）2=0，
∴a=6，c=4，
且b=4，
∴b=c=4，a=6，
又∵42+42≠62，
∴△ABC是等腰三角形．
故选A．
点评：本题考查了因式分解的应用、勾股定理的逆定理、非负数的性质，解题的关键是把b=8-c代入另一个已知条件中进行配方处理．
练习册系列答案
相关题目
如图由13个相同的正方形构成，若在标明字母的点之间连上线段，则（∠FPB+∠APC+∠APD+∠APE）+（∠EQA+∠FQ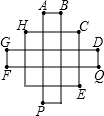
H+∠FQC+∠GQA）=（ ）
H+∠FQC+∠GQA）=（ ）| A、540° | B、450° |
| C、405° | D、360° |
我们来探究“雪花曲线”的有关问题：如图1是长为1的正三角形，现将它作如下变换：取三角形各边的三等分点向形外作没有底边的等边三角形，这样得到一个六角星（如图2）；继续对六角星各边施行相同的变换，得到“雪花形”（如图3）．如此继续下去，第4次变换后得到的图形的周长应等于（ ）
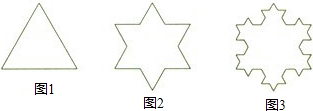
A、
| ||
B、
| ||
C、
| ||
D、
|
设
=
，则(
+
) ÷
=（ ）
| b |
| a+b |
| a-b |
| 3a-b |
| 2a2+b2 |
| 2a2-b2 |
| a2-8b2 |
| a2+8b2 |
| 2a |
| 3b |
A、
| ||
B、-
| ||
C、-
| ||
D、
|
礼堂第一排有a个座位，后面每排多1个座位，礼堂共有15排座位，则这礼堂的座位总数有（ ）个．
| A、15a+105 |
| B、15a+136 |
| C、15a+120 |
| D、14a+105 |