题目内容
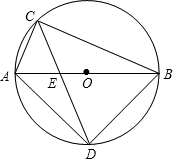 ⊙O中,AB为直径,CD平分∠ACB交⊙O于D,求证:
⊙O中,AB为直径,CD平分∠ACB交⊙O于D,求证:| CA+CB |
| CD |
| 2 |
考点:圆周角定理
专题:证明题
分析:根据直径所对的圆周角是直角,以及角平分线的定义可得∠ACD=∠BCD=45°,过A作AM⊥CD,过B作BN⊥CD,垂足分别为M、N,得到△ACM与△BCN都是等腰直角三角形,根据等腰直角三角形斜边与直角边的关系可得CM=
AC,BN=
BC,再利用角角边定理证明△ADM与△BDN全等,根据全等三角形对应边相等得到DN=AM,所以DN=CM,从而得到CM+CN=DN+CN=CD,整理即可得证.
| ||
| 2 |
| ||
| 2 |
解答:证明:过A作AM⊥CD,过B作BN⊥CD,垂足分别为M、N,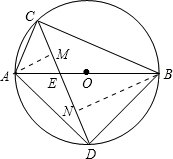
∵AB为直径,CD平分∠ACB交⊙O于D,
∴∠ACD=∠BCD=45°,
∴△ACM与△BCN都是等腰直角三角形,AD=BD,
在Rt△ACM中,CM=
AC,在Rt△BCN中,CN=
BC,
∴CM+CN=
(AC+BC),
∵AB是直径,
∴∠ADB=90°,
∴∠ADM+∠BDN=90°,
又∵∠BDN+∠DBN=90°,
∴∠ADM=∠DBN,
在△ADM与△BDN中,
,
∴△ADM≌△BDN(AAS),
∴DN=AM,
又∵AM=CM(等腰直角三角形两直角边相等),
∴CM=DN,
∴CD=CN+DN=CN+CM=
(AC+BC),
∴
=
.

∵AB为直径,CD平分∠ACB交⊙O于D,
∴∠ACD=∠BCD=45°,
∴△ACM与△BCN都是等腰直角三角形,AD=BD,
在Rt△ACM中,CM=
| ||
| 2 |
| ||
| 2 |
∴CM+CN=
| ||
| 2 |
∵AB是直径,
∴∠ADB=90°,
∴∠ADM+∠BDN=90°,
又∵∠BDN+∠DBN=90°,
∴∠ADM=∠DBN,
在△ADM与△BDN中,
|
∴△ADM≌△BDN(AAS),
∴DN=AM,
又∵AM=CM(等腰直角三角形两直角边相等),
∴CM=DN,
∴CD=CN+DN=CN+CM=
| ||
| 2 |
∴
| AC+BC |
| CD |
| 2 |
点评:本题考查了圆周角定理,全等三角形的判定与性质,以及等腰直角三角形的判定与性质,作出辅助线构造出等腰直角三角形与全等三角形是解题的关键.

练习册系列答案
相关题目
如图由13个相同的正方形构成,若在标明字母的点之间连上线段,则(∠FPB+∠APC+∠APD+∠APE)+(∠EQA+∠FQ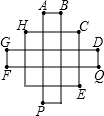 H+∠FQC+∠GQA)=( )
H+∠FQC+∠GQA)=( )
 H+∠FQC+∠GQA)=( )
H+∠FQC+∠GQA)=( )| A、540° | B、450° |
| C、405° | D、360° |
设
=
,则(
+
) ÷
=( )
| b |
| a+b |
| a-b |
| 3a-b |
| 2a2+b2 |
| 2a2-b2 |
| a2-8b2 |
| a2+8b2 |
| 2a |
| 3b |
A、
| ||
B、-
| ||
C、-
| ||
D、
|
 如图,奥运五环标志里,包含了圆与圆位置关系中的( )
如图,奥运五环标志里,包含了圆与圆位置关系中的( )| A、相切,内含 |
| B、外切,内含 |
| C、外离,相交 |
| D、相切,相交 |
在∠AOB的角平分线上有一点P,在OA上有一点M,在OB上有一点N,若PM=PN,则△POM与△PON( )
| A、一定全等 | B、可能全等 |
| C、一定不全等 | D、无法确定 |
礼堂第一排有a个座位,后面每排多1个座位,礼堂共有15排座位,则这礼堂的座位总数有( )个.
| A、15a+105 |
| B、15a+136 |
| C、15a+120 |
| D、14a+105 |
下列式子中的各字母均为实数,其中不可能成立的式子是( )
| A、(a-b)2=a2-b2 | ||
| B、x3+x2=x5 | ||
| C、x-1=-x | ||
D、
|