题目内容
等腰△ABC的一个底角为30°,一条边长为2
,则△ABC的周长为 .
| 3 |
考点:等腰三角形的性质,含30度角的直角三角形,勾股定理
专题:推理填空题,分类讨论
分析:根据已知的边可以是腰长,也可以是底边的长度,然后作出底边上的高,再根据30°角所对的直角边等于斜边的一半,分别利用勾股定理进行求解即可.
解答: 解:如图,作AD⊥BC,D为垂足,则
解:如图,作AD⊥BC,D为垂足,则
BD=CD=
AB(等腰三角形三线合一),
①当已知边为腰长时,AB=2
,∠B=30°,
∴AD=
AB=
,
在Rt△ABD中,BD=
=
=3,
∴BC=2BD=2×3=6,
∴△ABC的周长=6+2
×2=6+4
,
②当已知边为底边时,BD=
×2
=
,∠B=30°,
在Rt△ABD中,AB2=AD2+BD2,
即AB2=
AB2+
2,
解得AB=2,
∴△ABC的周长=2×2+2
=4+2
,
综上所述,△ABC的周长为6+4
或4+2
.
故答案为:6+4
或4+2
.
 解:如图,作AD⊥BC,D为垂足,则
解:如图,作AD⊥BC,D为垂足,则BD=CD=
| 1 |
| 2 |
①当已知边为腰长时,AB=2
| 3 |
∴AD=
| 1 |
| 2 |
| 3 |
在Rt△ABD中,BD=
| AB2-AD2 |
(2
|
∴BC=2BD=2×3=6,
∴△ABC的周长=6+2
| 3 |
| 3 |
②当已知边为底边时,BD=
| 1 |
| 2 |
| 3 |
| 3 |
在Rt△ABD中,AB2=AD2+BD2,
即AB2=
| 1 |
| 4 |
| 3 |
解得AB=2,
∴△ABC的周长=2×2+2
| 3 |
| 3 |
综上所述,△ABC的周长为6+4
| 3 |
| 3 |
故答案为:6+4
| 3 |
| 3 |
点评:本题考查了等腰三角形的性质,直角三角形30°所对的直角边等于斜边的一半的性质,勾股定理,因为已知边不明确,要注意分情况进行讨论求解,避免漏解而导致出错.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
如图由13个相同的正方形构成,若在标明字母的点之间连上线段,则(∠FPB+∠APC+∠APD+∠APE)+(∠EQA+∠FQ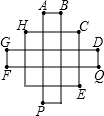 H+∠FQC+∠GQA)=( )
H+∠FQC+∠GQA)=( )
 H+∠FQC+∠GQA)=( )
H+∠FQC+∠GQA)=( )| A、540° | B、450° |
| C、405° | D、360° |
 图中所示为“三角城”的街道图.若某人欲从O点走到B点,但只能沿着街道向东、北或东北走,则共有
图中所示为“三角城”的街道图.若某人欲从O点走到B点,但只能沿着街道向东、北或东北走,则共有 如图,在△ABC中,∠A=40°,∠B=65°,则∠C=
如图,在△ABC中,∠A=40°,∠B=65°,则∠C=