题目内容
有一枚牌子,正面是1,反面是0,则将牌子连续丢两次,则两次的数字之和为1的概率是( )
A、
| ||
B、
| ||
C、
| ||
| D、1 |
考点:列表法与树状图法
专题:计算题,应用题
分析:本题是一个古典概型,试验发生包含的事件是将一枚牌子连续抛掷两次,以0表示出现反面,用1表示出现正面,列举出所有结果,满足条件的事件是一次正面和一次反面,从前面列举出的结果可知,根据概率公式得到结果.
解答:解:由题意知本题是一个古典概型,
∵试验发生包含的事件是将一枚牌子连续抛掷两次,
以0表示出现反面,用1表示出现正面,
则有(0,0)(0,1)(1,1)(1,0)
共有4种结果,
满足条件的事件是一次正面和一次反面,从前面列举出的结果可知有2种结果,
∴根据古典概型概率公式得到P=
=
,
故选B.
∵试验发生包含的事件是将一枚牌子连续抛掷两次,
以0表示出现反面,用1表示出现正面,
则有(0,0)(0,1)(1,1)(1,0)
共有4种结果,
满足条件的事件是一次正面和一次反面,从前面列举出的结果可知有2种结果,
∴根据古典概型概率公式得到P=
| 2 |
| 4 |
| 1 |
| 2 |
故选B.
点评:本题考查古典概型,是一个典型的古典概型问题,本题可以列举出试验发生包含的事件,也可以列举出满足条件的事件,是一个基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知x3+y3-z3=96,xyz=4,x2+y2+z2-xy+xz+yz=12,则x+y-z=( )
| A、6 | B、7 | C、8 | D、9 |
用长度为2l的材料围成一个矩形场地,中间有2个隔墙,要使矩形的面积最大,则隔墙的长度为( )
A、
| ||
B、
| ||
C、
| ||
| D、l |
如图由13个相同的正方形构成,若在标明字母的点之间连上线段,则(∠FPB+∠APC+∠APD+∠APE)+(∠EQA+∠FQ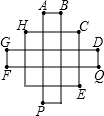 H+∠FQC+∠GQA)=( )
H+∠FQC+∠GQA)=( )
 H+∠FQC+∠GQA)=( )
H+∠FQC+∠GQA)=( )| A、540° | B、450° |
| C、405° | D、360° |
我们来探究“雪花曲线”的有关问题:如图1是长为1的正三角形,现将它作如下变换:取三角形各边的三等分点向形外作没有底边的等边三角形,这样得到一个六角星(如图2);继续对六角星各边施行相同的变换,得到“雪花形”(如图3).如此继续下去,第4次变换后得到的图形的周长应等于( )
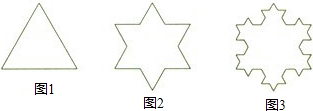

A、
| ||
B、
| ||
C、
| ||
D、
|
 如图,奥运五环标志里,包含了圆与圆位置关系中的( )
如图,奥运五环标志里,包含了圆与圆位置关系中的( )| A、相切,内含 |
| B、外切,内含 |
| C、外离,相交 |
| D、相切,相交 |