题目内容
2．已知（x+y-3）2+|xy-2|=0，求x3y-2x2y2+xy3的值．分析 根据非负数的和为零，可得x、y的值，根据分解因式，可得xy[（x+y）2-4xy]，再根据代数式求值，可得答案．
解答 解：由（x+y-3）2+|xy-2|=0，得
x+y-3=0，且xy-2=0．
解得x+y=3，xy=2．
x3y-2x2y2+xy3=xy（x2-2xy+y2）=xy[（x+y）2-4xy]，
当x+y=3，xy=2时，原式=2×[32-4×2]=2×1=2．
点评 本题考查了因式分解，利用差的平方等于和的平方减乘积的4倍是解题关键．
练习册系列答案
阅读快车系列答案
相关题目
12．若分式$\frac{1}{{{x^2}+2x+m}}$无论x取何实数总有意义，则函数y=（m+1）x+（m-1）的图象经过第（ ）象限．
| A． | 一、二、三 | B． | 一、三、四 | C． | 二、三、四， | D． | 一、二、四 |
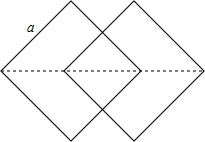如图，这是由一个边长为a的正方形沿一条对角线的方向平移$\frac{\sqrt{2}a}{2}$得到的图案．
如图，∠AOB=35°，∠BOC=90°，OD是∠AOC的平分线，求∠BOD的度数．