题目内容
5.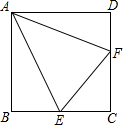 已知点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,且正方形ABCD的面积是△AEF的面积的$\frac{5}{2}$倍,EF=4,则AB的长是5.
已知点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,且正方形ABCD的面积是△AEF的面积的$\frac{5}{2}$倍,EF=4,则AB的长是5.
分析 将△ABE绕点A逆时针旋转90°,得△ADE',根据旋转的性质,判定△AEF≌△AE'F(SAS),得出EF=E'F,设正方形ABCD的边长为a,构建方程即可解决问题.
解答 解:将△ABE绕点A逆时针旋转90°,得△ADE',则
AE=AE',∠BAE=∠DAE',∠ADE'=90°=∠ADF,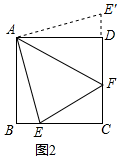
∴E',D,F在同一直线上,
∵正方形ABCD中,∠EAF=45°,
∴∠BAE+∠DAF=45°=∠DAE'+∠DAF=∠E'AF,
∴∠EAF=∠E'AF,
又∵AF=AF,
∴△AEF≌△AE'F(SAS),
∴EF=E'F,设正方形ABCD的边长为a,
∴S△AEF=S△AFE′=$\frac{1}{2}$•4•a=2a,
则有a2=$\frac{5}{2}$•2a,
∵a≠0,
∴a=5,
故答案为5.
点评 本题考查正方形的性质、全等三角形的判定和性质、一元二次方程等知识,解题的关键是学会用旋转法添加辅助线,属于中考参考题型.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
17. 如图,2×3的网格是由边长为a的小正方形组成,那么图中阴影部分的面积是( )
如图,2×3的网格是由边长为a的小正方形组成,那么图中阴影部分的面积是( )
 如图,2×3的网格是由边长为a的小正方形组成,那么图中阴影部分的面积是( )
如图,2×3的网格是由边长为a的小正方形组成,那么图中阴影部分的面积是( )| A. | a2 | B. | $\frac{3}{2}$a2 | C. | 2a2 | D. | 3a2 |
15.一家游泳馆的游泳收费标准为25元/次,若购买会员年卡,可享受如下优惠:
例如,购买A类会员卡,一年内游泳20次,消费50+20×20=450元,若一年内在该游泳馆消费500元,则游泳次数最多的办卡方式是( )
| 会员年卡类型 | 办卡费用(元) | 每次游泳收费(元) |
| A类 | 50 | 20 |
| B类 | 150 | 15 |
| C类 | 300 | 10 |
| A. | 购买A类会员年卡 | B. | 购买B类会员年卡 | C. | 购买C类会员年卡 | D. | 不购买会员年卡 |
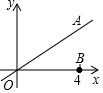 如图,直线OA是一次函数y=$\frac{x}{2}$的图象,点B的坐标是(4,0),点C在直线OA上且△OBC为等腰三角形,满足条件的C点共有4个.
如图,直线OA是一次函数y=$\frac{x}{2}$的图象,点B的坐标是(4,0),点C在直线OA上且△OBC为等腰三角形,满足条件的C点共有4个.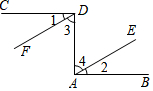 如图,已知CD⊥DA,DA⊥AB,∠1=∠2.试说明DF∥AE.请你完成下列填空,把证明过程补充完整.
如图,已知CD⊥DA,DA⊥AB,∠1=∠2.试说明DF∥AE.请你完成下列填空,把证明过程补充完整.