题目内容
14.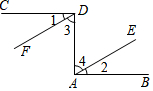 如图,已知CD⊥DA,DA⊥AB,∠1=∠2.试说明DF∥AE.请你完成下列填空,把证明过程补充完整.
如图,已知CD⊥DA,DA⊥AB,∠1=∠2.试说明DF∥AE.请你完成下列填空,把证明过程补充完整.证明:∵CD⊥DA,DA⊥AB,,
∴∠CDA=90°,∠DAB=90° (垂直定义).
∴∠1+∠3=90°,∠2+∠4=90°.
又∵∠1=∠2,
∴∠3=∠4 (等角的余角相等),
∴DF∥AE (内错角相等,两直线平行).
分析 先根据垂直的定义,得到∠1+∠3=90°,∠2+∠4=90°,再根据等角的余角相等,得出∠3=∠4,最后根据内错角相等,两直线平行进行判定即可.
解答 证明:∵CD⊥DA,DA⊥AB,
∴∠CDA=90°,∠DAB=90°,(垂直定义)
∴∠1+∠3=90°,∠2+∠4=90°.
又∵∠1=∠2,
∴∠3=∠4,(等角的余角相等)
∴DF∥AE.(内错角相等,两直线平行)
故答案为:CD⊥DA,DA⊥AB,垂直定义,∠3=∠4,等角的余角相等,内错角相等,两直线平行.
点评 本题主要考查了平行线的判定以及垂直的定义,解题时注意:内错角相等,两直线平行.

练习册系列答案
相关题目
6. 如图,∠1=15°,∠AOC=90°,点B,O,D在同一直线上,则∠2的度数为( )
如图,∠1=15°,∠AOC=90°,点B,O,D在同一直线上,则∠2的度数为( )
 如图,∠1=15°,∠AOC=90°,点B,O,D在同一直线上,则∠2的度数为( )
如图,∠1=15°,∠AOC=90°,点B,O,D在同一直线上,则∠2的度数为( )| A. | 75° | B. | 30° | C. | 45° | D. | 105° |
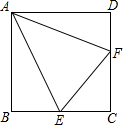 已知点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,且正方形ABCD的面积是△AEF的面积的$\frac{5}{2}$倍,EF=4,则AB的长是5.
已知点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,且正方形ABCD的面积是△AEF的面积的$\frac{5}{2}$倍,EF=4,则AB的长是5. 已知如图,∠ABC=60°,BM平分∠ABC,过BM上任意一点D(D点不与B点重合)作BC的平行线交AB于点E.
已知如图,∠ABC=60°,BM平分∠ABC,过BM上任意一点D(D点不与B点重合)作BC的平行线交AB于点E.
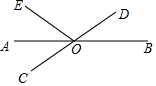 如图,直线AB,CD相交于点O,OA平分∠EOC,若∠EOC=70°.
如图,直线AB,CD相交于点O,OA平分∠EOC,若∠EOC=70°.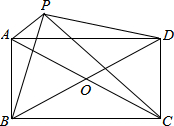 如图,?ABCD中,对角线AC、BD相交于点O,点P是四边形外一点,且PA⊥PC,PB⊥PD,垂足为P,且PA2+PC2=PB2+PD2.求证:四边形ABCD为矩形.
如图,?ABCD中,对角线AC、BD相交于点O,点P是四边形外一点,且PA⊥PC,PB⊥PD,垂足为P,且PA2+PC2=PB2+PD2.求证:四边形ABCD为矩形.