题目内容
10.计算:(1)$\sqrt{48}$-9$\sqrt{\frac{1}{3}}$+$\frac{6}{\sqrt{27}}$
(2)($\frac{\sqrt{5}+1}{2}$)2-($\frac{\sqrt{5}-1}{2}$)2.
分析 (1)先把二次根式化为最简二次根式,然后分母有理化后合并即可;
(2)利用平方差公式计算.
解答 解:(1)原式=4$\sqrt{3}$-3$\sqrt{3}$+$\frac{6}{3\sqrt{3}}$
=$\sqrt{3}$+$\frac{2\sqrt{3}}{3}$
=$\frac{5\sqrt{3}}{3}$;
(2)原式=[($\frac{\sqrt{5}+1}{2}$)+($\frac{\sqrt{5}-1}{2}$)]•[($\frac{\sqrt{5}+1}{2}$)-($\frac{\sqrt{5}-1}{2}$)]
=$\sqrt{5}$•1
=$\sqrt{5}$.
点评 本题考查了二次根式的混合运算:先把二次根式化为最简二次根式,然后进行二次根式的乘除运算,再合并即可.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.

练习册系列答案
相关题目
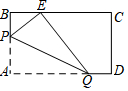 如图,矩形纸片ABCD,AB=3,AD=5,折叠纸片,使点A落在BC边上的E处,折痕为PQ,当点E在BC边上移动时,折痕的端点P、Q也随之移动.若限定点P、Q分别在AB、AD边上移动,则点E在BC边上可移动的最大距离为2.
如图,矩形纸片ABCD,AB=3,AD=5,折叠纸片,使点A落在BC边上的E处,折痕为PQ,当点E在BC边上移动时,折痕的端点P、Q也随之移动.若限定点P、Q分别在AB、AD边上移动,则点E在BC边上可移动的最大距离为2. 如图,已知点O为∠CAB与∠ACD的平分线的交点,OE⊥AC于E,若OE=2,则点O到AB的距离与点O到CD的距离之和是4.
如图,已知点O为∠CAB与∠ACD的平分线的交点,OE⊥AC于E,若OE=2,则点O到AB的距离与点O到CD的距离之和是4.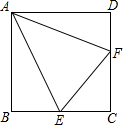 已知点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,且正方形ABCD的面积是△AEF的面积的$\frac{5}{2}$倍,EF=4,则AB的长是5.
已知点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,且正方形ABCD的面积是△AEF的面积的$\frac{5}{2}$倍,EF=4,则AB的长是5.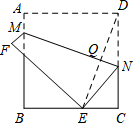 如图,正方形ABCD的边长为4,点M、N分别在AB、CD上.将该纸片沿MN折叠,使点D落在边BC上,设落点为E,折痕MN与DE相交于Q.
如图,正方形ABCD的边长为4,点M、N分别在AB、CD上.将该纸片沿MN折叠,使点D落在边BC上,设落点为E,折痕MN与DE相交于Q. 已知如图,∠ABC=60°,BM平分∠ABC,过BM上任意一点D(D点不与B点重合)作BC的平行线交AB于点E.
已知如图,∠ABC=60°,BM平分∠ABC,过BM上任意一点D(D点不与B点重合)作BC的平行线交AB于点E.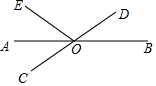 如图,直线AB,CD相交于点O,OA平分∠EOC,若∠EOC=70°.
如图,直线AB,CD相交于点O,OA平分∠EOC,若∠EOC=70°.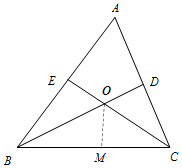 如图,△ABC中,∠A=60°,∠ABC的平分线BD与∠ACB的平分线CE相交于点O.
如图,△ABC中,∠A=60°,∠ABC的平分线BD与∠ACB的平分线CE相交于点O.