题目内容
 如图所示,在△ABC中,DE∥AB∥FG,且FA=2CD=2DF.若△ABC的面积为64,则四边形ABGF的面积S等于( )
如图所示,在△ABC中,DE∥AB∥FG,且FA=2CD=2DF.若△ABC的面积为64,则四边形ABGF的面积S等于( )| A、24 | B、36 | C、48 | D、54 |
考点:相似三角形的判定与性质
专题:
分析:先由FA=2CD=2DF,根据平行线分线段成比例定理得到CF:AC=1:2,再根据平行于三角形一边的直线截三角形所得的三角形与原三角形相似得到△CDE∽△CAB,根据相似三角形的性质得S△CFG:S△CAB=CF2:CA2=1:4,再根据△ABC的面积为64,即可计算出△CFG的面积,进而即可求得四边形ABGF的面积S.
解答:解:∵DE∥AB∥FG,且FA=2CD=2DF,
∴FA=FC,
∴
=
,
∵AB∥FG,
∴△CFG∽△CAB,
∴S△CFG:S△CAB=CF2:CA2=1:4,
∵△ABC的面积为64,
∴△CFG的面积S=64×
=16.
∴四边形ABGF的面积S=64-16=48.
故选C.
∴FA=FC,
∴
| FC |
| AC |
| 1 |
| 2 |
∵AB∥FG,
∴△CFG∽△CAB,
∴S△CFG:S△CAB=CF2:CA2=1:4,
∵△ABC的面积为64,
∴△CFG的面积S=64×
| 1 |
| 4 |
∴四边形ABGF的面积S=64-16=48.
故选C.
点评:本题考查了三角形相似的判定与性质:平行于三角形一边的直线截三角形所得的三角形与原三角形相似;相似三角形对应边的比等于相似比,相似三角形面积的比等于相似比的平方.

练习册系列答案
相关题目
 已知二次函数y=ax2+bx+c的图象如图所示,并设M=|a+b+c|-|a-b+c|+|2a+b|-|2a-b|,则( )
已知二次函数y=ax2+bx+c的图象如图所示,并设M=|a+b+c|-|a-b+c|+|2a+b|-|2a-b|,则( )| A、M<0 |
| B、M=0 |
| C、M>0 |
| D、不能确定M为正、负或为0 |
 如图所示,D,E,F分别是△ABC三边的中点,G是AE的中点,BE与DF、DG分别交于P,Q两点,则PQ:BE=( )
如图所示,D,E,F分别是△ABC三边的中点,G是AE的中点,BE与DF、DG分别交于P,Q两点,则PQ:BE=( )| A、1:2 | B、1:4 |
| C、1:6 | D、1:8 |
 如图,在Rt△ABC中,∠C=90°,AD是△CAB的平分线,DE垂直平分AB,若CD=3,则BD=
如图,在Rt△ABC中,∠C=90°,AD是△CAB的平分线,DE垂直平分AB,若CD=3,则BD=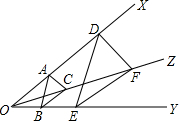 如图,点A,D在∠XOY的边OX上,点B,E在OY边上,射线OZ在∠XOY内,且点C,F在OZ上,AC∥DF,BC∥EF.
如图,点A,D在∠XOY的边OX上,点B,E在OY边上,射线OZ在∠XOY内,且点C,F在OZ上,AC∥DF,BC∥EF. 如图,长方形内有两个面积分别为5,2的正方形,求阴影部分的面积.
如图,长方形内有两个面积分别为5,2的正方形,求阴影部分的面积.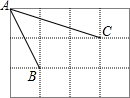 如图,在正方形网格中,小正方形的边长均为1,点A、B、C都是格点,则cos∠BAC=
如图,在正方形网格中,小正方形的边长均为1,点A、B、C都是格点,则cos∠BAC=