题目内容
 已知二次函数y=ax2+bx+c的图象如图所示,并设M=|a+b+c|-|a-b+c|+|2a+b|-|2a-b|,则( )
已知二次函数y=ax2+bx+c的图象如图所示,并设M=|a+b+c|-|a-b+c|+|2a+b|-|2a-b|,则( )| A、M<0 |
| B、M=0 |
| C、M>0 |
| D、不能确定M为正、负或为0 |
考点:二次函数图象与系数的关系
专题:
分析:由抛物线的位置确定解析式中系数符号特征,判定a、b、c的符号,并由x=±1,推出相应y值的正负性.
解答:解:由图可知a<0,c>0,
对称轴-1<-
<0,则b<0,可得2a+b<0,2a-b>0,
当x=1时,a+b+c<0,当x=-1时,a-b+c>0,
且由图可看出|a+b+c|<|a-b+c|,
∴M=|a+b+c|-|a-b+c|+|2a+b|-|2a-b|<0.
故选A.
对称轴-1<-
| b |
| 2a |
当x=1时,a+b+c<0,当x=-1时,a-b+c>0,
且由图可看出|a+b+c|<|a-b+c|,
∴M=|a+b+c|-|a-b+c|+|2a+b|-|2a-b|<0.
故选A.
点评:本题考查了二次函数的图象与系数的关系,难度一般,在解题中常常要运用图形做出判断,判断出各个参数的正负.

练习册系列答案
相关题目
 如图所示,在矩形ABCD中,DE⊥AC于点E,设∠ADE=a,且cosa=
如图所示,在矩形ABCD中,DE⊥AC于点E,设∠ADE=a,且cosa=| 3 |
| 5 |
| A、3 | ||
B、
| ||
C、
| ||
D、
|
下列四组数中不能构成直角三角形的一组是( )
A、1,2,
| ||||
B、
| ||||
| C、13,12,5 | ||||
D、1,3,
|
 如图所示,在△ABC中,DE∥AB∥FG,且FA=2CD=2DF.若△ABC的面积为64,则四边形ABGF的面积S等于( )
如图所示,在△ABC中,DE∥AB∥FG,且FA=2CD=2DF.若△ABC的面积为64,则四边形ABGF的面积S等于( )| A、24 | B、36 | C、48 | D、54 |
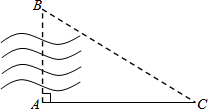 如图,A、B两点在河两岸,为了测算这两点之间的距离,小华在河岸边选定一点C,测得AC=100米,∠A=90°,∠C=30°,则AB≈
如图,A、B两点在河两岸,为了测算这两点之间的距离,小华在河岸边选定一点C,测得AC=100米,∠A=90°,∠C=30°,则AB≈ 如图,已知点O在直线CD上,当∠1和∠2满足条件
如图,已知点O在直线CD上,当∠1和∠2满足条件 如图,以原点O为顶点的等腰直角三角形ABO中,∠BAO=90°,反比例函数
如图,以原点O为顶点的等腰直角三角形ABO中,∠BAO=90°,反比例函数