题目内容
6.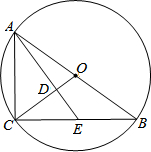 如图,⊙O是Rt△ABC的外接圆,∠ACB=90°,E为BC上一点,连接AE与OC交于点D,∠CAE=∠CBA.
如图,⊙O是Rt△ABC的外接圆,∠ACB=90°,E为BC上一点,连接AE与OC交于点D,∠CAE=∠CBA.(1)求证:AE⊥OC;
(2)若⊙O的半径为5,AE的长为6,求AD的长.
分析 (1)根据直角三角形的性质和垂直的定义即可得到结论;
(2)由△ACE∽△BCA,得到比例式$\frac{CE}{AC}=\frac{AE}{AB}$=$\frac{6}{10}$=$\frac{3}{5}$,设AC=5x,CE=3x,由勾股定理求得AE=$\sqrt{(5x)^{2}+(3x)^{2}}$=$\sqrt{34}$x=6,得到AC=$\frac{15\sqrt{34}}{17}$,再由三角形相似即可得到结果.
解答 (1)证明:∵∠ACB=90°,
∴∠CBA+∠CAB=90°,
∵∠CAE=∠CBA,
∴∠CAE+∠CAB=90°,
∵OA=OC,
∴∠CAO=∠ACO,
∴∠CAE+∠ACO=90°,
∴∠ADC=90°,
∴AE⊥OC;
(2)解:∵∠CAE=∠CBA,∠ACB=∠ACE,
∴△ACE∽△BCA,
∴$\frac{CE}{AC}=\frac{AE}{AB}$=$\frac{6}{10}$=$\frac{3}{5}$,
∴设AC=5x,CE=3x,
∴AE=$\sqrt{(5x)^{2}+(3x)^{2}}$=$\sqrt{34}$x=6,
∴x=$\frac{3\sqrt{34}}{17}$,
∴AC=$\frac{15\sqrt{34}}{17}$,
∵∠CAE=∠CAD,∠ACE=∠ADC,
∴△ACD∽△AEC,
∴$\frac{AC}{AE}=\frac{AD}{AC}$,
∴AD=$\frac{A{C}^{2}}{AE}$=$\frac{75}{17}$.
点评 本题考查了相似三角形的判定和性质,勾股定理,垂直的定义,找准相似三角形是解题的关键.

练习册系列答案
相关题目
17.先化简,再求值:a(a+b)(a-b)-a(a2-3b)+(a-b)2-a(a-b2),其中a=-2,b=$\sqrt{12}$-$\root{3}{8}$+($\frac{1}{2}$)-1.
15.反比例函数y=$\frac{k}{x}$(k<0),下列说法正确的是( )
| A. | 可以取任意实数 | B. | 函数图象在第一、三象限 | ||
| C. | 图象过点(1,k)和(-k,-1) | D. | 与函数y=4x的图象有两个交点 |
16.在平面直角坐标系中,点P(3,2)在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
 如图所示,矩形的长是4cm,宽是3cm,如果将其长与宽都增加x cm,那么面积增加y cm2
如图所示,矩形的长是4cm,宽是3cm,如果将其长与宽都增加x cm,那么面积增加y cm2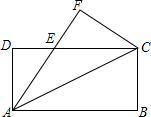 如图,将矩形纸片ABCD沿对角线AC折叠,使点B落到点F的位置,AF与CD交于点E
如图,将矩形纸片ABCD沿对角线AC折叠,使点B落到点F的位置,AF与CD交于点E 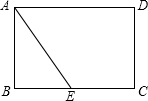 如图,有一张矩形纸片ABCD,AB=4cm,BC=6cm,点E是BC的中点.实施操作:将纸片沿直线AE折叠,使点B落在梯形AECD内,记为点B′.
如图,有一张矩形纸片ABCD,AB=4cm,BC=6cm,点E是BC的中点.实施操作:将纸片沿直线AE折叠,使点B落在梯形AECD内,记为点B′.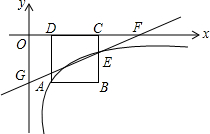 如图,正方形ABCD的顶点C,D在x轴的正半轴上,反比例函数y=$\frac{k}{x}$(k≠0)在第四象限的图象经过顶点A(m,-2)和BC边上的点E(n,-$\frac{2}{3}$),过点E的直线l交x轴于点F,交y轴于点G(0,-2),则点F的坐标是($\frac{9}{2}$,0).
如图,正方形ABCD的顶点C,D在x轴的正半轴上,反比例函数y=$\frac{k}{x}$(k≠0)在第四象限的图象经过顶点A(m,-2)和BC边上的点E(n,-$\frac{2}{3}$),过点E的直线l交x轴于点F,交y轴于点G(0,-2),则点F的坐标是($\frac{9}{2}$,0).