题目内容
1.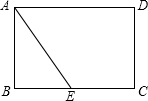 如图,有一张矩形纸片ABCD,AB=4cm,BC=6cm,点E是BC的中点.实施操作:将纸片沿直线AE折叠,使点B落在梯形AECD内,记为点B′.
如图,有一张矩形纸片ABCD,AB=4cm,BC=6cm,点E是BC的中点.实施操作:将纸片沿直线AE折叠,使点B落在梯形AECD内,记为点B′.(1)用尺规在图中作出△AEB′(保留作图痕迹);
(2)求B′、C两点之间的距离.
分析 (1)分别以A、E为圆心,AB、EB为半径作弧,交点为B′,再连接AB′、EB′即可;
(2)连接BB′,交AE于点F,连接B′C;由折叠的性质得出BF=B′F,证出EF为△BCB′的中位线,得出EF=$\frac{1}{2}$B′C,由勾股定理求出AE、得出cos∠BEF,在Rt△BEF中,由三角函数求出EF,即可得出B′C的长.
解答 解:(1)作法:①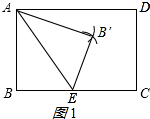 分别以A、E为圆心,AB、EB为半径作弧,交点为B′,
分别以A、E为圆心,AB、EB为半径作弧,交点为B′,
②连接AB′、EB′,得△AEB′;
如图1所示:
(2)连接BB′交AE于点F,连接B′C;
如图2所示:
由折叠的性质得:BF=B′F,
即F为BB′的中点,
∵E是BC的中点,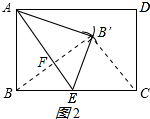
∴EF为△BCB′的中位线,
∴EF=$\frac{1}{2}$B′C,
在Rt△ABE中,AB=4cm,BE=3cm,
∴AE=$\sqrt{A{B}^{2}+B{E}^{2}}$=5cm,cos∠BEF=$\frac{3}{5}$,
在Rt△BEF中,EF=BE×cos∠BEF=3×$\frac{3}{5}$=$\frac{9}{5}$cm,
∴B′C=2EF=$\frac{18}{5}$cm.
点评 本题考查了翻折变换的性质、勾股定理、三角形中位线定理、三角函数;熟练掌握翻折变换的性质,并能进行作图与推理计算是解决问题的关键.

练习册系列答案
 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案 激活思维优加课堂系列答案
激活思维优加课堂系列答案
相关题目
10.若反比例函数y=$\frac{k}{x}$的图象分布在第二、四象限,则k的取值范围为( )
| A. | k>0 | B. | k>1 | C. | k<0 | D. | k<1 |
 如图,菱形ABCD的周长为20,一条对角线AC长为8,另一条对角线BD长为6.
如图,菱形ABCD的周长为20,一条对角线AC长为8,另一条对角线BD长为6. 已知:△ABC内接于⊙O,过点B作直线EF,AB为非直径的弦,且EF是⊙O的切线
已知:△ABC内接于⊙O,过点B作直线EF,AB为非直径的弦,且EF是⊙O的切线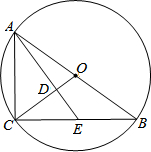 如图,⊙O是Rt△ABC的外接圆,∠ACB=90°,E为BC上一点,连接AE与OC交于点D,∠CAE=∠CBA.
如图,⊙O是Rt△ABC的外接圆,∠ACB=90°,E为BC上一点,连接AE与OC交于点D,∠CAE=∠CBA.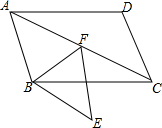 如图,点F在?ABCD的对角线AC上,过点F、B分别作AB、AC的平行线相交于点E,连接BF,∠ABF=∠FBC+∠FCB.
如图,点F在?ABCD的对角线AC上,过点F、B分别作AB、AC的平行线相交于点E,连接BF,∠ABF=∠FBC+∠FCB.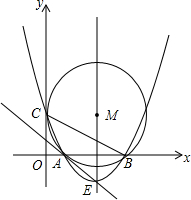 如图,在平面直角坐标系中,点M的坐标是(5,4),⊙M与y轴相切于点C,与x轴相交于A,B两点.
如图,在平面直角坐标系中,点M的坐标是(5,4),⊙M与y轴相切于点C,与x轴相交于A,B两点.