题目内容
5.解方程组(1)$\left\{\begin{array}{l}{x-2y=4}\\{2x-y=6}\end{array}\right.$
(2)$\left\{\begin{array}{l}{\stackrel{x+y=8}{y+z=6}}\\{x+z=4}\end{array}\right.$.
分析 (1)根据加减消元法消去x,可以得到y的值,再将y的值代入原方程组即可求得x的值,本题得以解决;
(2)根据加减消元法,将原方程组变为二元,然后再变为一元一次方程,本题得以解决.
解答 解:(1)$\left\{\begin{array}{l}{x-2y=4}&{①}\\{2x-y=6}&{②}\end{array}\right.$
①×2-②,得
-3y=2
解得,y=$-\frac{2}{3}$,
将y=-$\frac{2}{3}$代入①,得
x=$\frac{8}{3}$
故原方程组的解是$\left\{\begin{array}{l}{x=\frac{8}{3}}\\{y=-\frac{2}{3}}\end{array}\right.$;
(2)$\left\{\begin{array}{l}{x+y=8}&{①}\\{y+z=6}&{②}\\{x+z=4}&{③}\end{array}\right.$
①-②,得
x-z=2④
③+④,得
x=3
将x=3代入①,得
y=5,
将x=3代入③,得
z=1
故原方程组的解是
$\left\{\begin{array}{l}{x=3}\\{y=5}\\{z=1}\end{array}\right.$.
点评 本题考查解二元一次方程组、解三元一次方程组,解题的关键是明确解方程组的方法,会用消元法解方程组.

练习册系列答案
相关题目
10.已知不等式4x-a≤0的正整数解是1,2,则a的取值范围是( )
| A. | 8<a<12 | B. | 8≤a<12 | C. | 8<a≤12 | D. | 8≤a≤12 |
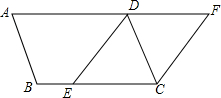 如图,?ABCD,点E是BC边的一点,将边AD延长至点F,使∠AFC=∠DEC,连接CF、DE.
如图,?ABCD,点E是BC边的一点,将边AD延长至点F,使∠AFC=∠DEC,连接CF、DE.