题目内容
16．已知关于x的不等式（3-a）x＞2的解集为x＜$\frac{2}{3-a}$，则a的取值范囤是a＞3．分析 根据不等式两边都除以（3-a），不等号的方向发生改变判断出3-a＜0，然后求解即可．
解答 解：∵关于x的不等式（3-a）x＞2的解集为x＜$\frac{2}{3-a}$，
∴3-a＜0，
∴a＞3．
故答案为：a＞3．
点评 本题考查了解一元一次不等式，熟记不等式的基本性质并判断出x的系数小于0是解题的关键．
练习册系列答案
相关题目
如图，在边长为4的正方形ABCD中，以BC为直径的半圆交对角线BD于E，则图中阴影部分的面积为8．
1．
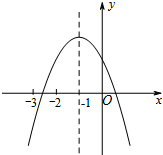如图是二次函数y=ax2+bx+c图象的一部分，过点（x1，0），-3＜x1＜-2，对称轴为直线x=-1．给出四个结论：①abc＞0；②2a+b=0；③b2＞4ac；④3b+2c＞0，其中正确的结论有（ ）
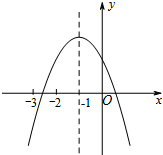如图是二次函数y=ax2+bx+c图象的一部分，过点（x1，0），-3＜x1＜-2，对称轴为直线x=-1．给出四个结论：①abc＞0；②2a+b=0；③b2＞4ac；④3b+2c＞0，其中正确的结论有（ ）| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
6．若点A（-3，-1）在反比例函数y=$\frac{k}{x}$的图象上，则分式方程$\frac{k}{x}$=$\frac{2}{x-2}$的解是（ ）
| A． | x=-6 | B． | x=6 | C． | x=-$\frac{6}{5}$ | D． | x=$\frac{6}{5}$ |