题目内容
17.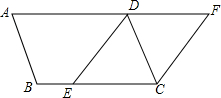 如图,?ABCD,点E是BC边的一点,将边AD延长至点F,使∠AFC=∠DEC,连接CF、DE.
如图,?ABCD,点E是BC边的一点,将边AD延长至点F,使∠AFC=∠DEC,连接CF、DE.(1)求证:四边形DECF是平行四边形;
(2)若AB=13,DF=14,tanA=$\frac{12}{5}$,求CF的长.
分析 (1)根据平行四边形的性质得出AD∥BC,求出DE∥CF,根据平行四边形的判定得出即可;
(2)过D作DM⊥EC于M,根据勾股定理求出DM和CM,求出DE,即可求出答案.
解答 (1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠ADE=∠DEC,
∵∠AFC=∠DEC,
∴∠AFC=∠ADE,
∴DE∥CF,
∵AD∥BC,
∴DF∥CE,
∴四边形DECF是平行四边形;
(2)解:过D作DM⊥EC于M,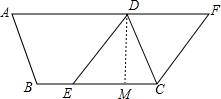 则∠DMC=∠DME=90°,
则∠DMC=∠DME=90°,
∵四边形ABCD是平行四边形,
∴DC=AB=13,∠DCB=∠A,
∵tanA=$\frac{12}{5}$,
∴tan∠DCB=$\frac{12}{5}$=$\frac{DM}{MC}$,
设DM=12xCM=5x,
由勾股定理得:(12x)2+(5x)2=132,
解得:x=1,
即CM=5,DM=12,
∵CE=14,
∴EM=14-5=9,
在Rt△DME中,由勾股定理得:DE=$\sqrt{1{2}^{2}+{9}^{2}}$=15,
∵四边形DECF是平行四边形,
∴CF=DE=15.
点评 本题考查了平行四边形的性质和判定,勾股定理,解直角三角形的应用,能灵活运用性质进行推理和计算是解此题的关键.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案
相关题目
6.若点A(-3,-1)在反比例函数y=$\frac{k}{x}$的图象上,则分式方程$\frac{k}{x}$=$\frac{2}{x-2}$的解是( )
| A. | x=-6 | B. | x=6 | C. | x=-$\frac{6}{5}$ | D. | x=$\frac{6}{5}$ |
7.小强统计了他家3月份打电话的次数及通话时间,这些数据均不超过20分钟,并列出了频数分布表:
(1)小强家3月份一共打了多少次电话?
(2)求通话时间不超过12分钟的频数和频率?
| 通话时长(x分钟) | 0<x≤4 | 4<x≤8 | 8<x≤12 | 12<x≤16 | 16<x≤20 |
| 频数(通话次数) | 28 | 14 | 6 | 16 | 10 |
(2)求通话时间不超过12分钟的频数和频率?