题目内容
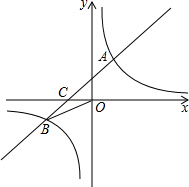 已知:如图,在平面直角坐标系中,一次函数y=ax+b (a≠0)的图象与反比例函数y=
已知:如图,在平面直角坐标系中,一次函数y=ax+b (a≠0)的图象与反比例函数y=| k |
| x |
(1)求该反比例函数和一次函数的解析式;
(2)在x轴上有一点E(O点除外),使得△BCE与△BCO的面积相等,求出点E的坐标.
考点:反比例函数与一次函数的交点问题
专题:
分析:(1)先将点A坐标代入反比例函数y=
(k≠0),求得k的值,再将点B坐标代入反比例函数y=
(k≠0),即可得出n的值,再把AB两点的坐标代入一次函数y=ax+b (a≠0)求得a,b的值即可;
(2)因为一次函数y=ax+b(a≠0)的图象与x轴交于C点,所以求得C(-2,0),再因为S△BCE=S△BCO,所以CE=OC=2,即可得出OE=4,则E(-4,0).
| k |
| x |
| k |
| x |
(2)因为一次函数y=ax+b(a≠0)的图象与x轴交于C点,所以求得C(-2,0),再因为S△BCE=S△BCO,所以CE=OC=2,即可得出OE=4,则E(-4,0).
解答:解:(1)把A(2,4)代入y=
中得k=8,
所以反比例函数解析式为y=
…(1分)
点B的坐标为(n,-2)代入y=
中,得n=-4,
∴B(-4,-2)…(1分)
把A(2,4),B(-4,-2)两点代入y=ax+b中,
得a=1 b=2,所以一次函数解析式为y=x+2 …(1分)
(2)∵一次函数y=ax+b(a≠0)的图象与x轴交于C点,
∴当y=0时,x=-2,
∴C(-2,0),即OC=2 …(1分)
∵S△BCE=S△BCO,
∴CE=OC=2,…(1分)
∴OE=4,即E(-4,0)…(1分)
| k |
| x |
所以反比例函数解析式为y=
| 8 |
| x |
点B的坐标为(n,-2)代入y=
| 8 |
| x |
∴B(-4,-2)…(1分)
把A(2,4),B(-4,-2)两点代入y=ax+b中,
得a=1 b=2,所以一次函数解析式为y=x+2 …(1分)
(2)∵一次函数y=ax+b(a≠0)的图象与x轴交于C点,
∴当y=0时,x=-2,
∴C(-2,0),即OC=2 …(1分)
∵S△BCE=S△BCO,
∴CE=OC=2,…(1分)
∴OE=4,即E(-4,0)…(1分)
点评:本题综合考查反比例函数与一次函数的交点问题.先由点的坐标求函数解析式,然后解由解析式组成的方程组求出交点的坐标,体现了数形结合的思想.

练习册系列答案
相关题目
四个数-
,0,3.14,
中,为无理数的是( )
| 1 |
| 2 |
| 3 |
A、-
| ||
| B、0 | ||
| C、3.14 | ||
D、
|
下列说法正确的是( )
| A、三角形的内心是这个三角形三条边中垂线的交点 |
| B、矩形的对角线相等的逆命题是真命题 |
| C、一组数据2、9、7、5、4、8、5、3的中位数是5 |
| D、正六边形的外角和是720度 |
下列运算中正确的是( )
| A、a2+a3=a5 | ||
B、
| ||
| C、(2a)3=6a3 | ||
| D、-(3x-2)(-3x-2)=4-9x2 |
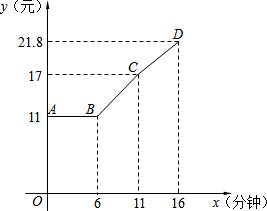 某市出租车按里程计费标准为:不超过3公里部分,计费11元,超过3公里部分,按每公里2.4元计费.现在在此基础上,如果车速不超过12公里/小时,那么再加收0.48元/分钟,这项费用叫做“双计费”.图中三段折线表示某时间段内,一辆出租车的计费总额y(元)与行驶时间x(分钟)的函数关系(出租车在每段上均匀速行驶).
某市出租车按里程计费标准为:不超过3公里部分,计费11元,超过3公里部分,按每公里2.4元计费.现在在此基础上,如果车速不超过12公里/小时,那么再加收0.48元/分钟,这项费用叫做“双计费”.图中三段折线表示某时间段内,一辆出租车的计费总额y(元)与行驶时间x(分钟)的函数关系(出租车在每段上均匀速行驶). 已知抛物线y=ax2-2ax-4与x轴交于点A、B(点A在点B的左侧),与y轴交于点C,△ABC的面积为12.
已知抛物线y=ax2-2ax-4与x轴交于点A、B(点A在点B的左侧),与y轴交于点C,△ABC的面积为12.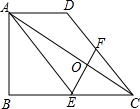 已知:如图,在梯形ABCD中,AD∥BC,∠ABC=90°,BC=2AD,点E是BC的中点、F是CD上的点,联结AE、EF、AC.
已知:如图,在梯形ABCD中,AD∥BC,∠ABC=90°,BC=2AD,点E是BC的中点、F是CD上的点,联结AE、EF、AC.