题目内容
15．若关于x的一元二次方程ax2+bx+6=0的一个根为x=2，则代数式2a+b+6的值为3．分析 根据一元二次方程的解，把x=2代入ax2+bx+6=0可得到2a+b=-3，然后利用整体代入的方法计算代数式2a+b+6的值．
解答 解：把x=2代入ax2+bx+6=0得4a+2b+6=0，则2a+b=-3，
所以2a+b+6=-3+6=3．
故答案为3．
点评 本题考查了一元二次方程的解：能使一元二次方程左右两边相等的未知数的值是一元二次方程的解．
练习册系列答案
相关题目
5．下列各式中不能用公式法分解因式的是（ ）
| A． | x2-6x+9 | B． | -x2+y2 | C． | x2+2x+4 | D． | -x2+2xy-y2 |
6．方程$\frac{3}{x-2}$+$\frac{1}{2-x}$=1的解为（ ）
| A． | -1 | B． | 1 | C． | 4 | D． | 5 |
3．
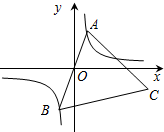如图，己知点A是双曲线y=$\frac{k}{x}$（k＞0）上的一个动点，连AO并延长交另一分支于点B，以AB为边作等边△ABC，点C在第四象限．随着点A的运动，点C的位置也不断变化，但点C始终在双曲线y=$\frac{m}{x}$（m＜0）上运动，则m与k的关系是（ ）
如图，己知点A是双曲线y=$\frac{k}{x}$（k＞0）上的一个动点，连AO并延长交另一分支于点B，以AB为边作等边△ABC，点C在第四象限．随着点A的运动，点C的位置也不断变化，但点C始终在双曲线y=$\frac{m}{x}$（m＜0）上运动，则m与k的关系是（ ）| A． | m=-k | B． | m=-$\sqrt{3}$k | C． | m=-2k | D． | m=-3k |
10．下列计算正确的是（ ）
| A． | x+x2=x3 | B． | 2x-3x=-x | C． | （x2）3=x5 | D． | x6÷x3=x2 |
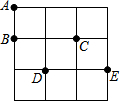在3×3的方格纸中，点A，B，C，D，E分别位于如图所示的小正方形格点上．
如图，已知AD⊥BC于D，EG⊥BC于G，∠1=∠E．试判断∠2与∠3的数量关系．