Question

20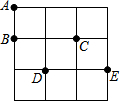．在3×3的方格纸中，点A，B，C，D，E分别位于如图所示的小正方形格点上．
（1）在点A，B，C，D，E中任取四个点为顶点直接在图上画一个中心对称的四边形；
（2）从A，B，C三个点中先任取一个点，在余下的两个点中再取一个点，将所取的这两点与点D，E为顶点构成四边形，求所得四边形中面积为2的概率（用树状图或列表法求解）．

Answer 1

分析 （1）根据中心 对称图形的定义作图即可得；
（2）画树状图列出所有可能结果，再根据概率公式求解可得．

解答 解：（1）如图，四边形BDEC即为所求，


（2）先后选取A，B，C的树状图如图所示

又∵只有四边形DECB面积为2，
∴所画四边形面积为2的概率为P=$\frac{2}{6}$=$\frac{1}{3}$．

点评 此题主要考查了利用树状图求概率及中心对称图形，根据已知正确列举出所有结果，进而得出概率是解题关键．