题目内容
3.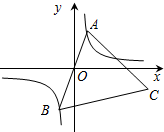 如图,己知点A是双曲线y=$\frac{k}{x}$(k>0)上的一个动点,连AO并延长交另一分支于点B,以AB为边作等边△ABC,点C在第四象限.随着点A的运动,点C的位置也不断变化,但点C始终在双曲线y=$\frac{m}{x}$(m<0)上运动,则m与k的关系是( )
如图,己知点A是双曲线y=$\frac{k}{x}$(k>0)上的一个动点,连AO并延长交另一分支于点B,以AB为边作等边△ABC,点C在第四象限.随着点A的运动,点C的位置也不断变化,但点C始终在双曲线y=$\frac{m}{x}$(m<0)上运动,则m与k的关系是( )| A. | m=-k | B. | m=-$\sqrt{3}$k | C. | m=-2k | D. | m=-3k |
分析 设点A的坐标为(a,$\frac{k}{a}$),连接OC,则OC⊥AB,表示出OC,过点C作CD⊥x轴于点D,设出点C坐标,在Rt△OCD中,利用勾股定理可得出x2的值,进而得出结论.
解答 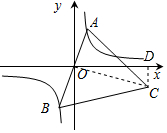 解:设A(a,$\frac{k}{a}$),
解:设A(a,$\frac{k}{a}$),
∵点A与点B关于原点对称,
∴OA=OB,
∵△ABC为等边三角形,
∴AB⊥OC,OC=$\sqrt{3}$AO,
∵AO=$\sqrt{{a}^{2}+(\frac{k}{a})^{2}}$,
∴CO=$\sqrt{3{a}^{2}+\frac{3{k}^{2}}{{a}^{2}}}$,
过点C作CD⊥x轴于点D,
则可得∠AOD=∠OCD(都是∠COD的余角),
设点C的坐标为(x,y),则tan∠AOD=tan∠OCD,即$\frac{\frac{k}{a}}{a}$=$\frac{x}{-y}$
解得y=-$\frac{{a}^{2}x}{k}$.
在Rt△COD中,CD2+OD2=OC2,即y2+x2=3a2+$\frac{3{k}^{2}}{{a}^{2}}$,将y=-$\frac{{a}^{2}x}{k}$代入得,x2=$\frac{3{k}^{2}}{{a}^{2}}$,
∴x=$\frac{\sqrt{3}k}{a}$,y=-$\frac{{a}^{2}x}{k}$=-$\frac{{a}^{2}}{k}$•$\frac{\sqrt{3}k}{a}$=-$\sqrt{3}$a,
∴m=xy=$\frac{\sqrt{3}k}{a}$•(-$\sqrt{3}$a)=-3k.
故选D.
点评 本题考查的是反比例函数图象上点的坐标特点,熟知反比例函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
13.化简$\frac{x}{x-y}$$-\frac{y}{x+y}$的结果为( )
| A. | $\frac{2xy}{{x}^{2}-{y}^{2}}$ | B. | $-\frac{2xy}{{x}^{2}-{y}^{2}}$ | C. | $\frac{{x}^{2}+{y}^{2}}{{x}^{2}-{y}^{2}}$ | D. | 1 |
18.将0.0000026用科学记数法表示为( )
| A. | 2.6×106 | B. | 0.26×10-5 | C. | 2.6×10-6 | D. | 2.6×10-7 |
12.云南高铁自开通以来,发展速度不断加快,现已成为云南市民主要出行方式之一.今年五一期间安全运输乘客约5460000人次.用科学记数法表示5460000为( )
| A. | 5.46×107 | B. | 5.46×106 | C. | 5.5×106 | D. | 546×104 |
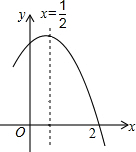 如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,对称轴为x=$\frac{1}{2}$,且经过点(2,0).下列说法:①abc<0;②-2b+c=0;③4a+2b+c<0;④若(-$\frac{5}{2}$,y1),($\frac{5}{2}$,y2)是抛物线上的两点,则y1<y2;⑤$\frac{1}{4}$a+$\frac{1}{2}$b>m(am+b)(其中m≠$\frac{1}{2}$).其中说法正确的是( )
如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,对称轴为x=$\frac{1}{2}$,且经过点(2,0).下列说法:①abc<0;②-2b+c=0;③4a+2b+c<0;④若(-$\frac{5}{2}$,y1),($\frac{5}{2}$,y2)是抛物线上的两点,则y1<y2;⑤$\frac{1}{4}$a+$\frac{1}{2}$b>m(am+b)(其中m≠$\frac{1}{2}$).其中说法正确的是( ) 如图所示的几何体是由一个正方体切去一个小正方体形成,其主视图为( )
如图所示的几何体是由一个正方体切去一个小正方体形成,其主视图为( )


