题目内容
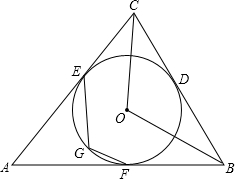 如图,圆O是△ABC的内切圆,D、E、F为切点,G为弧EF上的一点,请判断∠EGF与∠BOC是否相等,并说明理由.
如图,圆O是△ABC的内切圆,D、E、F为切点,G为弧EF上的一点,请判断∠EGF与∠BOC是否相等,并说明理由.考点:三角形的内切圆与内心
专题:
分析:利用切线的性质得出∠BOD=∠BDF,同理可得:∠COD=∠CDE,再利用四点共圆的性质求出即可.
解答: 解:∠EGF=∠BOC,
解:∠EGF=∠BOC,
理由:连接OD、ED、DF
∵⊙O是△ABC的内切圆,
∴BD=BF,∠OBF=∠OBD,
∴OB⊥DF,
∴∠BDF=90°-∠OBD,
∵BD切⊙O于点D,OD是⊙O半径,
∴OD⊥BC,
∴∠BOD=90°-∠OBD,
∴∠BOD=∠BDF,
同理可得:∠COD=∠CDE,
即∠BOC=∠BOD+∠COD=∠BDF+∠CDE,
∵∠EDF+∠BDF+∠CDE=180°,
∴∠BOC+∠EDF=180°,
∵D、E、G、F四点共圆,
∴∠EGF+∠EDF=180°,
∴∠EGF=∠BOC.
 解:∠EGF=∠BOC,
解:∠EGF=∠BOC,理由:连接OD、ED、DF
∵⊙O是△ABC的内切圆,
∴BD=BF,∠OBF=∠OBD,
∴OB⊥DF,
∴∠BDF=90°-∠OBD,
∵BD切⊙O于点D,OD是⊙O半径,
∴OD⊥BC,
∴∠BOD=90°-∠OBD,
∴∠BOD=∠BDF,
同理可得:∠COD=∠CDE,
即∠BOC=∠BOD+∠COD=∠BDF+∠CDE,
∵∠EDF+∠BDF+∠CDE=180°,
∴∠BOC+∠EDF=180°,
∵D、E、G、F四点共圆,
∴∠EGF+∠EDF=180°,
∴∠EGF=∠BOC.
点评:此题主要考查了三角形内切圆与内心以及四点共圆,得出:∠COD=∠CDE,∠BOD=∠BDF是解题关键.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
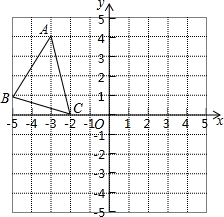 已知直角坐标系中的每个小方格的边长都是1个长度单位,△ABC的位置如图所示,现将△ABC向右平移5个单位,得到△A1B1C1,再向下平移4个单位,得到△A2B2C2.
已知直角坐标系中的每个小方格的边长都是1个长度单位,△ABC的位置如图所示,现将△ABC向右平移5个单位,得到△A1B1C1,再向下平移4个单位,得到△A2B2C2. 如图,在四边形ABCD中,AD∥BC,M为AB的中点,且DM平分∠ADC,CM平分∠BCD,AD=3cm,BC=7cm.求DC的长.
如图,在四边形ABCD中,AD∥BC,M为AB的中点,且DM平分∠ADC,CM平分∠BCD,AD=3cm,BC=7cm.求DC的长.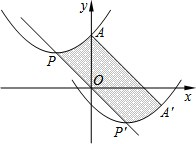 如图所示,抛物线的顶点P(-2,1),与y轴交于A(0,3),若平移该抛物线使其定点P沿直线移动到点P1(2,-1),点A的对应点为A′,则抛物线上PA段扫过的区域(阴影部分)的面积为
如图所示,抛物线的顶点P(-2,1),与y轴交于A(0,3),若平移该抛物线使其定点P沿直线移动到点P1(2,-1),点A的对应点为A′,则抛物线上PA段扫过的区域(阴影部分)的面积为