题目内容
16. 如图,已知∠1+∠2=180°,∠3=∠B,且∠AFE=50°.
如图,已知∠1+∠2=180°,∠3=∠B,且∠AFE=50°.(1)求证:FD∥AB;
(2)求∠ACB的度数.
分析 (1)根据平行线的判定定理即可得到结论;
(2)根据平行线的判定求出DF∥AB,根据平行线的性质得出∠3=∠AEF,求出∠AEF=∠B,根据平行线的判定推出EF∥BC,根据平行线的性质推出即可.
解答 解:(1)∵∠1+∠EDF=180°
∠1+∠2=180°
∴∠EDF=∠2
∴FD∥AB;
(2)由(1)知:DF∥AB
∴∠3=∠AEF
∵∠3=∠B
∴∠B=∠AEF
∴EF∥BC
∴∠ACB=∠AFE
∵∠AFE=50°
∴∠ACB=50°.
点评 本题考查了平行线的性质和判定的应用,能综合运用性质和判定进行推理是解此题的关键,难度适中.

练习册系列答案
相关题目
4.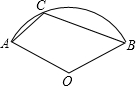 如图,扇形OAB的圆心角为120°,C是弧AB上一点,则∠ACB的度数为( )
如图,扇形OAB的圆心角为120°,C是弧AB上一点,则∠ACB的度数为( )
 如图,扇形OAB的圆心角为120°,C是弧AB上一点,则∠ACB的度数为( )
如图,扇形OAB的圆心角为120°,C是弧AB上一点,则∠ACB的度数为( )| A. | 240° | B. | 120° | C. | 90° | D. | 75° |
6.下列函数中,y是x的一次函数的是( )
| A. | y=$\sqrt{x}$ | B. | y=2x+11 | C. | y=x2+x+1 | D. | y=$\frac{1}{x}$ |
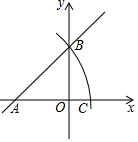 如图,在平面直角坐标系中,直线y=x+b交x轴于点A,交y轴于点B,以点A为圆心,线段AB长为半径作圆弧,交x轴正半轴于点C,若AC=$\sqrt{2}$,则b的值为1.
如图,在平面直角坐标系中,直线y=x+b交x轴于点A,交y轴于点B,以点A为圆心,线段AB长为半径作圆弧,交x轴正半轴于点C,若AC=$\sqrt{2}$,则b的值为1.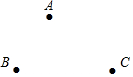 如图,已知点A、B、C.
如图,已知点A、B、C.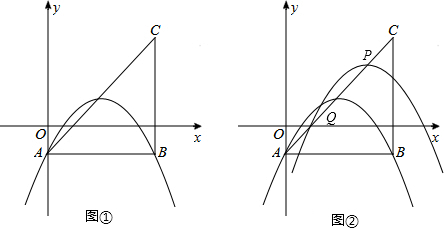
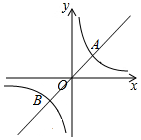 在平面直角坐标系xOy中,直线y=x与双曲线y=$\frac{k}{x}$(k≠0)的一个交点为A($\sqrt{6}$,m).
在平面直角坐标系xOy中,直线y=x与双曲线y=$\frac{k}{x}$(k≠0)的一个交点为A($\sqrt{6}$,m). 如图,在△ABC中,∠ACB=90°,CE⊥AB于点E,AD=AC,AF平分
如图,在△ABC中,∠ACB=90°,CE⊥AB于点E,AD=AC,AF平分