题目内容
8.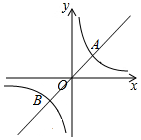 在平面直角坐标系xOy中,直线y=x与双曲线y=$\frac{k}{x}$(k≠0)的一个交点为A($\sqrt{6}$,m).
在平面直角坐标系xOy中,直线y=x与双曲线y=$\frac{k}{x}$(k≠0)的一个交点为A($\sqrt{6}$,m).(1)求k的值;
(2)将直线y=x向上平移1个单位长度,与x轴、y轴分别交于点C、D,与双曲线y=$\frac{k}{x}$(k≠0)在第一象限的交点记为Q.试猜想线段DQ和CD的数量关系,并证明你的猜想.
分析 (1)先根据直线y=x与双曲线y=$\frac{k}{x}$(k≠0)的一个交点为A($\sqrt{6}$,m),求得点A的坐标,进而代入反比例函数解析式得出k的值;
(2)先根据平移后的直线解析式求得C(-1,0),D(0,1),再令x+1=$\frac{6}{x}$,求得Q(2,3),进而得出线段DQ和CD的数量关系.
解答 解:(1)把A($\sqrt{6}$,m)代入直线y=x,可得
m=$\sqrt{6}$,
∴A($\sqrt{6}$,$\sqrt{6}$),
把A($\sqrt{6}$,$\sqrt{6}$)代入双曲线y=$\frac{k}{x}$,可得
k=6;
(2)DQ=2CD,
证明:将直线y=x向上平移1个单位长度,可得y=x+1,
∴C(-1,0),D(0,1),
即CO=DO=1,
∴CD=$\sqrt{2}$,
令x+1=$\frac{6}{x}$,解得x=2或-3,
∵点Q在第一象限,
∴Q(2,3),
∴DQ=$\sqrt{{2}^{2}+{2}^{2}}$=2$\sqrt{2}$,
∴DQ=2CD.
点评 本题考查了一次函数与反比例函数的交点问题,由点的坐标求函数的解析式以及直线平移规律.求反比例函数与一次函数的交点坐标,把两个函数关系式联立成方程组求解.

练习册系列答案
相关题目
13. 如图,如果CD是Rt△ABC的中线,∠ACB=90°,∠A=50°,那么∠CDB等于( )
如图,如果CD是Rt△ABC的中线,∠ACB=90°,∠A=50°,那么∠CDB等于( )
 如图,如果CD是Rt△ABC的中线,∠ACB=90°,∠A=50°,那么∠CDB等于( )
如图,如果CD是Rt△ABC的中线,∠ACB=90°,∠A=50°,那么∠CDB等于( )| A. | 100° | B. | 110° | C. | 120° | D. | 130° |
20.若$\sqrt{{a}^{3}+3{a}^{2}}$=-a$\sqrt{a+3}$,则a的取值范围是( )
| A. | -3≤a≤0 | B. | a≤0 | C. | a<0 | D. | a≥-3 |
17.若m>-1,则下列错误的是( )
| A. | 6m>-6 | B. | -5m>5 | C. | m+1>0 | D. | 1-m<2 |
 如图,已知∠1+∠2=180°,∠3=∠B,且∠AFE=50°.
如图,已知∠1+∠2=180°,∠3=∠B,且∠AFE=50°.