题目内容
19．解不等式组：$\left\{{\begin{array}{l}{2x-1＞3（x-1）}\\{\frac{5-x}{2}＜x+5}\end{array}}\right.$，并写出它的所有非负整数解．分析 首先解每个不等式，两个不等式的解集的公共部分就是不等式组的解集，然后确定非负整数解即可．
解答 解：$\left\{\begin{array}{l}{2x-1＞3（x-1）…①}\\{\frac{5-x}{2}＜x+5…②}\end{array}\right.$，
解①得x＜2，
解②得x＞-$\frac{5}{3}$．
则不等式组的解集是：-$\frac{5}{3}$＜x＜2．
则非负整数解是：0，1．
点评 本题考查的是一元一次不等式组的解，解此类题目常常要结合数轴来判断．还可以观察不等式的解，若x＞较小的数、＜较大的数，那么解集为x介于两数之间．
练习册系列答案
阅读快车系列答案
相关题目
9．方程（x-2）2+4=0的解是（ ）
| A． | x1=x2=0 | B． | x1=2，x2=-2 | C． | x1=0，x2=4 | D． | 没有实数根 |
10．据统计，2015年上海市全年接待国际旅游入境者共80016000人次，80016000用科学记数法表示是（ ）
| A． | 8.0016×106 | B． | 8.0016×107 | C． | 8.0016×108 | D． | 8.0016×109 |
7．下列函数中，图象经过第二象限的是（ ）
| A． | y=2x | B． | y=$\frac{2}{x}$ | C． | y=x-2 | D． | y=x2-2 |
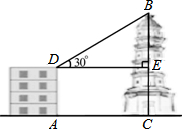如图，大楼AD和塔BC都垂直于地面AC，大楼AD高50米，和大楼AD相距90米的C处有一塔BC，某人在楼顶D处测得塔顶B的仰角∠BDE=30°，且∠BED=90°，求塔高BC．（结果保留整数，参考数据：$\sqrt{2}≈$1.41，$\sqrt{3}≈1.73$）