题目内容
8.如图1,平面直角坐标系中,抛物线y=ax2+bx+c与x轴交于A、B两点,与y轴交于点C,顶点为M.D在y轴上,OB=OD=3,OA=5.(1)试用含a的式子表示点M的坐标;
(2)若S△ABC-S△ACM=$\frac{50}{3}$;
①求抛物线y=ax2+bx+c的解析式;
②如图2,将△BOD绕点O沿逆时针方向旋转α(0°<α≤180°)得到△B′OD′,直线AD与BC相交于点Q,求点Q纵坐标的取值范围.
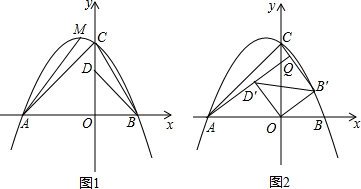
分析 (1)由线段长度,确定点A,B坐标代入y=ax2+bx+c即可用a表示抛物线,运用顶点公式即可求出点M坐标;
(2)①用a表示△ABC与△ACM的面积,根据题意列方程求解即可;
②根据题意分析出:以点O为圆心,以OB为半径作圆,当AD与圆O在第二象限内相切时,Q的纵坐标最大,当AD与圆O在第三象限内相切时,Q的纵坐标最小,
分别求解即可,求解时,先确定切点坐标,求出两条直线解析式,联立直线解方程组求出y的值即可.
解答 解:(1)由OB=OD=3,OA=5可得,
点A(-5,0),B(3,0),D(0,5),
设抛物线的解析式为y=a(x-3)×(x+5),
整理得:y=ax2+2ax-15a,
所以顶点M(-1,-16a);
(2)如图1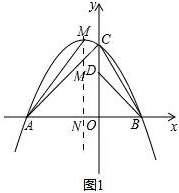
过点M作MN⊥x轴,垂足为N,交直线AC于点H,
y=ax2+2ax-15a,令x=0,解得:y=-15a,
所以:C(0,-15a)
设直线AC解析式为:y=mx+n,
由A(-5,0),C(0,-15a),坐标可得,$\left\{\begin{array}{l}{0=-5m+n}\\{n=-15a}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{m=-3a}\\{n=-15a}\end{array}\right.$,
所以直线AC:y=-3ax-15a,
由M(-1,-16a),可得,
点H(-1,-12a),
所以MH=-16a-(-12a)=-4a,
所以:S△ACM=$\frac{1}{2}×MH×({x}_{C}-{x}_{A})$=$\frac{1}{2}×(-4a)×5$=-10a,
S△ABC=$\frac{1}{2}×AB×OC$=-60a,
由S△ABC-S△ACM=$\frac{50}{3}$,
解得:a=-$\frac{1}{3}$,
所以:抛物线的解析式为:y=$-\frac{1}{3}{x}^{2}-\frac{2}{3}x+5$;
②如图2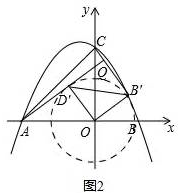
以点O为圆心,以OB为半径作圆,当AD与圆O在第二象限内相切时,Q的纵坐标最大,
此时,易求点D′的坐标为(-$\frac{9}{5},\frac{12}{5}$),点A(-5,0);点B′($\frac{12}{5},\frac{9}{5}$),
用两点法可求直线AD′解析式为:y=$\frac{3}{4}x+\frac{15}{4}$,
直线B′C的解析式为:$y=-\frac{4}{3}x+5$,
联立$\left\{\begin{array}{l}{y=\frac{3}{4}x+\frac{15}{4}}\\{y=-\frac{4}{3}x+5}\end{array}\right.$,
解得y=$\frac{21}{5}$,
如图3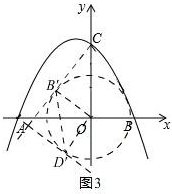
以点O为圆心,以OB为半径作圆,当AD与圆O在第三象限内相切时,Q的纵坐标最小,
此时易求点D′($-\frac{9}{5}$,$-\frac{12}{5}$),点A(-5,0);点B′(-$\frac{12}{5},\frac{9}{5}$),
用两点法可求直线AD′解析式为:$y=-\frac{3}{4}x-\frac{15}{4}$,
直线B′C的解析式为:$y=\frac{4}{3}x+5$,
联立$\left\{\begin{array}{l}{y=-\frac{3}{4}x-\frac{15}{4}}\\{y=\frac{4}{3}x+5}\end{array}\right.$,
解得:y=$-\frac{3}{5}$.
所以:点Q纵坐标的取值范围为:$-\frac{3}{5}$≤y≤$\frac{21}{5}$.
点评 此题主要考查二次函数的综合问题,会用已知点求解析式,会根据点的坐标表示三角形面积,会运用圆的知识分析解决旋转的相关问题是解题的关键.

 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案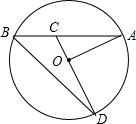 如图,已知AB是⊙O的弦,OA=4,∠A=30°,C是弦AB上任意一点(不与点A、B重合),连接CO并延长CO交⊙O于点D,连接BD.
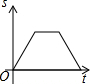
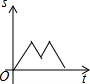
如图,已知AB是⊙O的弦,OA=4,∠A=30°,C是弦AB上任意一点(不与点A、B重合),连接CO并延长CO交⊙O于点D,连接BD. 星期天早晨茗茗陪爷爷出门散步,他们所走的路线组成一个等边三角形,如图所示,下列可以正确表示他们离家的距离s与时间t的函数图象的是( )
星期天早晨茗茗陪爷爷出门散步,他们所走的路线组成一个等边三角形,如图所示,下列可以正确表示他们离家的距离s与时间t的函数图象的是( )
 如图,在?ABCD中,对角线AC与BD交于点O,∠OBC=90°,AC=6,BD=4,则?ABCD的面积是4$\sqrt{5}$.
如图,在?ABCD中,对角线AC与BD交于点O,∠OBC=90°,AC=6,BD=4,则?ABCD的面积是4$\sqrt{5}$.