题目内容
4．
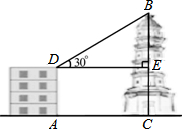如图，大楼AD和塔BC都垂直于地面AC，大楼AD高50米，和大楼AD相距90米的C处有一塔BC，某人在楼顶D处测得塔顶B的仰角∠BDE=30°，且∠BED=90°，求塔高BC．（结果保留整数，参考数据：$\sqrt{2}≈$1.41，$\sqrt{3}≈1.73$）
分析 在直角△BDE中利用三角函数求得BE的长，然后加上EC即可求得．
解答 解：∵在Rt△BDE中，tan∠BDE=$\frac{BE}{DE}，∠BDE={30^0}$，DE=90，
∴BE=DE×tan30°=30$\sqrt{3}$（米），
又∵BC=BE+CE=50+30$\sqrt{3}，\sqrt{3}$≈1.73
∴BC≈50+51.9≈102（米）．
答：塔BC高度约为102米．
点评 本题考查仰角的定义，要求学生能借助仰角构造直角三角形并解直角三角形．
练习册系列答案
相关题目
15．如果圆形纸片的直径是8cm，用它完全覆盖正六边形，那么正六边形的边长最大不能超过（ ）
| A． | 2cm | B． | 2$\sqrt{3}$cm | C． | 4cm | D． | 4$\sqrt{3}$Cm |
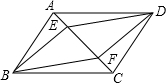如图，在?ABCD中，E、F为对角线AC上两点，且AE=CF．
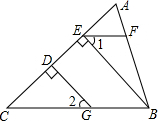如图所示，已知AB⊥BC，GD⊥AC于点D，BE⊥AC于点E，∠1=∠2，判断EF与AB的位置关系，并说明理由．
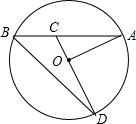如图，已知AB是⊙O的弦，OA=4，∠A=30°，C是弦AB上任意一点（不与点A、B重合），连接CO并延长CO交⊙O于点D，连接BD．