题目内容
2．
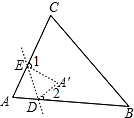如图所示，在折纸活动中，小明制作了一张△ABC纸片，点D，E分别在边AB，AC上，将△ABC沿着DE折叠压平，A与A′重合，若∠A=65°，则∠1+∠2=（ ）| A． | 210° | B． | 130° | C． | 115° | D． | 65° |
分析 先根据图形翻折变化的性质得出△ADE≌△A′DE，∠AED=∠A′ED，∠ADE=∠A′DE，再根据三角形内角和定理即可求出∠AED+∠ADE及∠A′ED+∠A′DE的度数，再根据平角的性质即可求出答案．
解答 解：∵△A′DE是△ADE翻折变换而成，
∴∠AED=∠A′ED，∠ADE=∠A′DE，∠A=∠A′=65°，
∴∠AED+∠ADE=∠A′ED+∠A′DE=180°-65°=115°，
∴∠1+∠2=360°-2×115°=130°．
故选：B．
点评 本题考查的是图形翻折变换的性质、三角形内角和定理；折叠是一种对称变换，它属于轴对称，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等．
练习册系列答案
相关题目
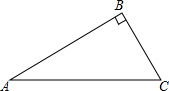已知，如图Rt△ABC中，AB=8，BC=6，求sin∠A和tan∠A．
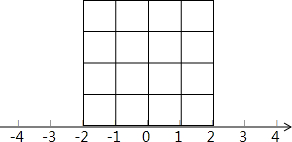（1）如图4×4的方格，每个小格的顶点叫做格点，若每个小正方形边长为1单位，请在方格中作一个正方形，同时满足下列两个条件：
已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，有下列结论：
为加强电动自行车质量监管，切实保障消费者的合法权益，2015年11月，河南开封市工商局对24个品牌批次的电动自行车进行抽查检验，其中抽查检验的某品牌的电动自行车如图所示，它的大灯M射出的光线MA，MB的与MN的夹角分别为76°和60°，MN⊥地面CD，MN=0.8m，图中的阴影部分表示在夜晚时，灯M所照射的范围．（提示：$\sqrt{3}$≈1.7，sin14°$≈\frac{6}{25}$，cos14°≈$\frac{97}{100}$，tan14$°≈\frac{1}{4}$）