题目内容
12.用适当的方法解下列方程:(1)2x2-10x=3
(2)(x+3)2=(1-2x)2
(3)(x+4)2=5(x+4)
(4)(x2-x)2-(x2-x)-2=0.
分析 (1)(2)把方程整理为一元二次方程的一般形式,再用公式法求出x的值即可;
(3)先移项,再提取公因式即可;
(4)令x2-x=a,利用因式分解法求助a的值,再求出x的值即可.
解答 解:(1)原方程可化为2x2-10x-3=0,
∵△=(-10)2-4×2×(-3)=100+24=124,
∴x=$\frac{10±\sqrt{124}}{2×3}$=$\frac{5±\sqrt{31}}{3}$,
∴x1=$\frac{5+\sqrt{31}}{3}$,x2=$\frac{5-\sqrt{31}}{3}$;
(2)原方程可化为3x2-10x-2=0,
∵△=(-10)2-4×3×(-2)=100+24=124,
∴x=$\frac{10±\sqrt{124}}{2×3}$=$\frac{5±\sqrt{31}}{3}$,
∴x1=$\frac{5+\sqrt{31}}{3}$,x2=$\frac{5-\sqrt{31}}{3}$;
(3)移项得,(x+4)2-5(x+4)=0,
提取公因式得,(x+4)(x-1)=0,
故x+4=0或x-1=0,解得x1=-4,x2=1;
(4)令x2-x=a,则原方程可化为a2-a-2=0,
因式分解得,(a+1)(a-2)=0,解得a=-1或a=2.
当a=-1时,x2-x=-1,即x2-x+1=0,
因为△=1-4=-3<0,所以此方程无解;
当a=2时,x2-x-2=0,即(x+1)(x-2)=0,解得x1=-1,x2=2.
点评 本题考查的是利用因式分解法解一元二次方程,在解答此题时要根据各方程的特点选择合适的方法.

练习册系列答案
 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
3. 如图,数轴上P点所表示的数可能是( )
如图,数轴上P点所表示的数可能是( )
 如图,数轴上P点所表示的数可能是( )
如图,数轴上P点所表示的数可能是( )| A. | $\sqrt{7}$ | B. | -3.2 | C. | -$\sqrt{7}$ | D. | -$\sqrt{10}$ |
2.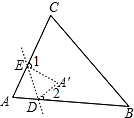 如图所示,在折纸活动中,小明制作了一张△ABC纸片,点D,E分别在边AB,AC上,将△ABC沿着DE折叠压平,A与A′重合,若∠A=65°,则∠1+∠2=( )
如图所示,在折纸活动中,小明制作了一张△ABC纸片,点D,E分别在边AB,AC上,将△ABC沿着DE折叠压平,A与A′重合,若∠A=65°,则∠1+∠2=( )
 如图所示,在折纸活动中,小明制作了一张△ABC纸片,点D,E分别在边AB,AC上,将△ABC沿着DE折叠压平,A与A′重合,若∠A=65°,则∠1+∠2=( )
如图所示,在折纸活动中,小明制作了一张△ABC纸片,点D,E分别在边AB,AC上,将△ABC沿着DE折叠压平,A与A′重合,若∠A=65°,则∠1+∠2=( )| A. | 210° | B. | 130° | C. | 115° | D. | 65° |
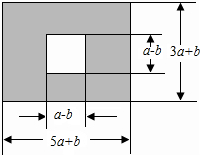 如图,某市有长为(5a+b)米,宽为(3a+b)米的长方形地块,计划将阴影部分用每块面积为2a平方米的草坪进行绿化,中间将修建一座雕像,则绿化至少需要这样的草坪多少块?并求出当a=3,b=-1时的值.
如图,某市有长为(5a+b)米,宽为(3a+b)米的长方形地块,计划将阴影部分用每块面积为2a平方米的草坪进行绿化,中间将修建一座雕像,则绿化至少需要这样的草坪多少块?并求出当a=3,b=-1时的值.