题目内容
7.化简:$\frac{{b}^{2}}{2a+b}\sqrt{\frac{4{a}^{3}+4{a}^{2}b+a{b}^{2}}{b}}$.分析 根据二次根式的性质进行化简即可.
解答 解:$\frac{{b}^{2}}{2a+b}\sqrt{\frac{4{a}^{3}+4{a}^{2}b+a{b}^{2}}{b}}$
=$\frac{{b}^{2}}{2a+b}$$\sqrt{\frac{ab(4{a}^{2}+4ab+{b}^{2})}{{b}^{2}}}$
=$\frac{{b}^{2}}{2a+b}$×$\frac{2a+b}{b}$×$\sqrt{ab}$
=b$\sqrt{ab}$.
点评 本题考查的是二次根式的化简求值,掌握二次根式的性质:$\sqrt{{a}^{2}}$=|a|是解题的关键.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
15.某商场有一批苹果,卖出的苹果质量x(kg)与售价y(元)的关系如下表:
(1)写出售价y(元)与卖出质量x(kg)之间的关系式;
(2)该商场若卖出苹果50kg,售价为多少元?
| 质量x(kg) | 1 | 2 | 3 | 4 | 5 | … |
| 售价y(元) | 2+0.1 | 4+0.2 | 6+0.3 | 8+0.4 | 10+0.5 | … |
(2)该商场若卖出苹果50kg,售价为多少元?
2.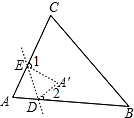 如图所示,在折纸活动中,小明制作了一张△ABC纸片,点D,E分别在边AB,AC上,将△ABC沿着DE折叠压平,A与A′重合,若∠A=65°,则∠1+∠2=( )
如图所示,在折纸活动中,小明制作了一张△ABC纸片,点D,E分别在边AB,AC上,将△ABC沿着DE折叠压平,A与A′重合,若∠A=65°,则∠1+∠2=( )
 如图所示,在折纸活动中,小明制作了一张△ABC纸片,点D,E分别在边AB,AC上,将△ABC沿着DE折叠压平,A与A′重合,若∠A=65°,则∠1+∠2=( )
如图所示,在折纸活动中,小明制作了一张△ABC纸片,点D,E分别在边AB,AC上,将△ABC沿着DE折叠压平,A与A′重合,若∠A=65°,则∠1+∠2=( )| A. | 210° | B. | 130° | C. | 115° | D. | 65° |
20.下列计算正确的是( )
| A. | (a3)2÷a5=a10 | B. | (a4)2÷a4=a2 | ||
| C. | (-5a2b3)•(-2a)=10a3b3 | D. | (-a3b)3÷$\frac{1}{2}{a^2}{b^2}=-2{a^4}$b |
 如图所示,要测量河两岸A,B间的距离,可用什么方法?并说明这样做的合理性.
如图所示,要测量河两岸A,B间的距离,可用什么方法?并说明这样做的合理性. 如图,已知A(-2,3)、B(-5,0)、C(-1,0).
如图,已知A(-2,3)、B(-5,0)、C(-1,0).