题目内容
10.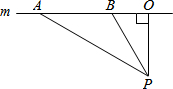 随着近几年我市私家车日越增多,超速行驶成为引发交通事故的主要原因之一.某中学数学活动小组为开展“文明驾驶、关爱家人、关爱他人”的活动,设计了如下检测公路上行驶的汽车速度的实验:先在公路旁边选取一点P,在笔直的车道m上确定点O,使PO和m垂直,测得PO的长等于21米,在m上的同侧取点A、B,使∠PAO=30°,∠PBO=60°.
随着近几年我市私家车日越增多,超速行驶成为引发交通事故的主要原因之一.某中学数学活动小组为开展“文明驾驶、关爱家人、关爱他人”的活动,设计了如下检测公路上行驶的汽车速度的实验:先在公路旁边选取一点P,在笔直的车道m上确定点O,使PO和m垂直,测得PO的长等于21米,在m上的同侧取点A、B,使∠PAO=30°,∠PBO=60°.(1)求A、B之间的路程(保留根号);
(2)已知本路段对校车限速为12米/秒若测得某校车从A到B用了2秒,这辆校车是否超速?请说明理由.
分析 (1)Rt△OPC与Rt△BOP中,先根据锐角三角函数的定义求出AO及BO的长,再根据AB=AO-BO即可得出结果;
(2)先根据汽车从A到B用时2秒求出其速度,再与已知相比较即可.
解答 解:(1)在Rt△AOP中,∵PO=21米,∠PAO=30°,
∴AO=$\frac{PO}{tan30°}$=$\frac{21}{\frac{\sqrt{3}}{3}}$=21$\sqrt{3}$(米);
在Rt△BOP中,∵PO=21米,∠PBO=60°,
∴BO=$\frac{PO}{tan60°}$=$\frac{21}{\sqrt{3}}$=7$\sqrt{3}$(米),
∴AB=AO-BO=14$\sqrt{3}$米;
(2)这辆校车超速;理由如下:
∵校车从A到B用时2秒,
∴速度为14$\sqrt{3}$÷2=7$\sqrt{3}$(米/秒)>12米/秒,
∴这辆校车在AB路段超速.
点评 此题考查了解直角三角形的应用问题.此题难度适中,解题的关键是把实际问题转化为数学问题求解,注意数形结合思想的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.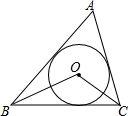 如图,已知⊙O是△ABC的内切圆,且∠ABC=50°,∠ACB=80°,则∠BOC=( )
如图,已知⊙O是△ABC的内切圆,且∠ABC=50°,∠ACB=80°,则∠BOC=( )
 如图,已知⊙O是△ABC的内切圆,且∠ABC=50°,∠ACB=80°,则∠BOC=( )
如图,已知⊙O是△ABC的内切圆,且∠ABC=50°,∠ACB=80°,则∠BOC=( )| A. | 100° | B. | 75° | C. | 115° | D. | 105° |
2.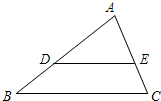 如图,△ABC中,DE∥BC,AD:DB=2:1,则△ADE与△ABC的面积之比是( )
如图,△ABC中,DE∥BC,AD:DB=2:1,则△ADE与△ABC的面积之比是( )
 如图,△ABC中,DE∥BC,AD:DB=2:1,则△ADE与△ABC的面积之比是( )
如图,△ABC中,DE∥BC,AD:DB=2:1,则△ADE与△ABC的面积之比是( )| A. | 4:1 | B. | 8:1 | C. | 4:9 | D. | 2:3 |
19.用配方法解一元二次方程x2-2x=1时,此方程可变形为( )
| A. | (x-1)2=0 | B. | (x-1)2=1 | C. | (x-1)2=2 | D. | (x+1)2=2 |
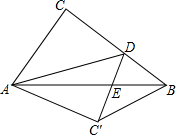 如图,在Rt△ABC中,∠ACB=90°,AB=5,AC=3,点D是BC上一动点,连结AD,将△ACD沿AD折叠,点C落在点C′,连结C′D交AB于点E,连结BC′.当△BC′D是直角三角形时,DE的长为$\frac{3}{2}$或$\frac{3}{4}$.
如图,在Rt△ABC中,∠ACB=90°,AB=5,AC=3,点D是BC上一动点,连结AD,将△ACD沿AD折叠,点C落在点C′,连结C′D交AB于点E,连结BC′.当△BC′D是直角三角形时,DE的长为$\frac{3}{2}$或$\frac{3}{4}$. 一个几何体,是由许多规格相同的小正方体堆积而成的,从正面看和从左面看的形状如图所示,要搭成这样的几何体,最少需用6块小正方体.
一个几何体,是由许多规格相同的小正方体堆积而成的,从正面看和从左面看的形状如图所示,要搭成这样的几何体,最少需用6块小正方体.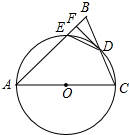 如图,在△ABC中,AB=AC,以AC为直径的⊙O交BC于点D,交AB于点E,过点D作DF⊥AB,垂足为点F,连接DE.
如图,在△ABC中,AB=AC,以AC为直径的⊙O交BC于点D,交AB于点E,过点D作DF⊥AB,垂足为点F,连接DE.