题目内容
15.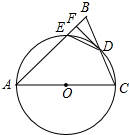 如图,在△ABC中,AB=AC,以AC为直径的⊙O交BC于点D,交AB于点E,过点D作DF⊥AB,垂足为点F,连接DE.
如图,在△ABC中,AB=AC,以AC为直径的⊙O交BC于点D,交AB于点E,过点D作DF⊥AB,垂足为点F,连接DE.(1)求证:直线DF与⊙O相切;
(2)若CD=3,BF=1,求AE的长.
分析 (1)连接OD,利用AB=AC,OD=OC,证得OD∥AB,易证DF⊥OD,故DF为⊙O的切线;
(2)根据内接四边形的性质得到∠AED+∠ACD=180°,由于∠AED+∠BED=180°,得到∠BED=∠ACD,由于∠B=∠B,推出△BED∽△BCA,根据相似三角形的性质得到$\frac{BD}{AB}=\frac{BE}{BC}$,∠DEB=∠ODC,得到∠B=∠DEB,求得BE=2BF=2,BD=CD=$\frac{1}{2}$BC=3,BC=6,即可得到结论.
解答 (1)证明:如图,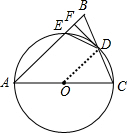 连接OD,
连接OD,
∵AB=AC,
∴∠B=∠C,
∵OD=OC,
∴∠ODC=∠C,
∴∠ODC=∠B,
∴OD∥AB,
∵DF⊥AB,
∴OD⊥DF,
∵点D在⊙O上,
∴直线DF与⊙O相切;
(2)解:∵四边形ACDE是⊙O的内接四边形,
∴∠AED+∠ACD=180°,
∵∠AED+∠BED=180°,
∴∠BED=∠ACD,
∵∠B=∠B,
∴△BED∽△BCA,
∴$\frac{BD}{AB}=\frac{BE}{BC}$,∠DEB=∠ODC,
∴∠B=∠DEB,
∴BD=DE,
∴BE=2BF=2,
∵OD∥AB,AO=CO,
∴BD=CD=$\frac{1}{2}$BC=3,
∴BC=6,
∴$\frac{3}{AB}=\frac{2}{6}$,
∴AB=9,
∴AE=AB-BE=7.
点评 此题考查切线的判定,三角形相似的判定与性质,圆内接四边形的性质,要证某线是圆的切线,已知此线过圆上某点,连接圆心和这点(即为半径),再证垂直即可.

练习册系列答案
相关题目
7.若a<0,$\frac{a}{b}$<0,且|a|>|b|,则( )
| A. | a<-b<b<-a | B. | a<b<-b<-a | C. | -a<-b<b<a | D. | -b<-a<b<a |
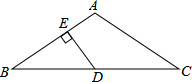 在△ABC中,AB=AC,∠A=120°,D是BC的中点,DE⊥AB,垂足是E,则AE:BE=1:3.
在△ABC中,AB=AC,∠A=120°,D是BC的中点,DE⊥AB,垂足是E,则AE:BE=1:3.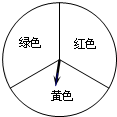 甲、乙两位同学玩转盘游戏,游戏规则:将圆盘平均分成三份,分别涂上红,黄,绿三种颜色,两位同学分别转动转盘两次(若压线,重新转).若两次指针指到的颜色
甲、乙两位同学玩转盘游戏,游戏规则:将圆盘平均分成三份,分别涂上红,黄,绿三种颜色,两位同学分别转动转盘两次(若压线,重新转).若两次指针指到的颜色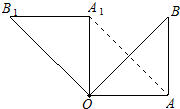 如图,在Rt△OAB,∠OAB=90°,OA=AB=6,将△OAB绕点O沿逆时针方向旋转90°得到△OA1B1.连结AA1
如图,在Rt△OAB,∠OAB=90°,OA=AB=6,将△OAB绕点O沿逆时针方向旋转90°得到△OA1B1.连结AA1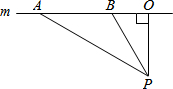 随着近几年我市私家车日越增多,超速行驶成为引发交通事故的主要原因之一.某中学数学活动小组为开展“文明驾驶、关爱家人、关爱他人”的活动,设计了如下检测公路上行驶的汽车速度的实验:先在公路旁边选取一点P,在笔直的车道m上确定点O,使PO和m垂直,测得PO的长等于21米,在m上的同侧取点A、B,使∠PAO=30°,∠PBO=60°.
随着近几年我市私家车日越增多,超速行驶成为引发交通事故的主要原因之一.某中学数学活动小组为开展“文明驾驶、关爱家人、关爱他人”的活动,设计了如下检测公路上行驶的汽车速度的实验:先在公路旁边选取一点P,在笔直的车道m上确定点O,使PO和m垂直,测得PO的长等于21米,在m上的同侧取点A、B,使∠PAO=30°,∠PBO=60°. ,那么它的实际车牌号是9689.
,那么它的实际车牌号是9689.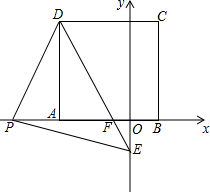 如图,在直角坐标系中,点A(-3,0)和点B(1,0)以AB为边在x轴上方作正方形ABCD,点P是x轴负半轴上一点,连接DP,过点P作DP的垂线与y轴负半轴交于点E,PD=PE,连接DE.
如图,在直角坐标系中,点A(-3,0)和点B(1,0)以AB为边在x轴上方作正方形ABCD,点P是x轴负半轴上一点,连接DP,过点P作DP的垂线与y轴负半轴交于点E,PD=PE,连接DE.