题目内容
 如图,已知AB⊥BC,AD⊥DE,BC与DE相交于点F,且BC=DE,AC=AE,连接CD、EB.求证:∠CDF=∠EBF.
如图,已知AB⊥BC,AD⊥DE,BC与DE相交于点F,且BC=DE,AC=AE,连接CD、EB.求证:∠CDF=∠EBF.考点:全等三角形的判定与性质
专题:证明题
分析:证出Rt△ABC≌Rt△ADE,推出AB=AD,∠ACB=∠AED,∠CAB=∠EAD,求出∠CAD=∠EAB,证出△CAD≌△EAB,推出∠ACD=∠AEB,即可得出答案.
解答:证明:∵AB⊥BC,AD⊥DE,
∴∠ADE=∠ABC,
在Rt△ABC和Rt△ADE中,
,
∴Rt△ABC≌Rt△ADE(HL),
∴AB=AD,∠ACB=∠AED,∠CAB=∠EAD,
∴∠CAB-∠DAB=∠EAD-∠DAB,
∴∠CAD=∠EAB,
在△CAD和△EAB中,
,
∴△CAD≌△EAB(SAS),
∴∠ACD=∠AEB,
∵∠ACB=∠AED,
∴∠CDF=∠EBF.
∴∠ADE=∠ABC,
在Rt△ABC和Rt△ADE中,
|
∴Rt△ABC≌Rt△ADE(HL),
∴AB=AD,∠ACB=∠AED,∠CAB=∠EAD,
∴∠CAB-∠DAB=∠EAD-∠DAB,
∴∠CAD=∠EAB,
在△CAD和△EAB中,
|
∴△CAD≌△EAB(SAS),
∴∠ACD=∠AEB,
∵∠ACB=∠AED,
∴∠CDF=∠EBF.
点评:本题考查了全等三角形的性质和判定的应用,主要考查学生的推理能力,题目比较好,难度适中.

练习册系列答案
相关题目
 我国是世界上严重缺水的国家之一,为了增强居民的节水意识,某自来水公司对居民用水采取以户为单位分段计费办法收费:即每月用水10吨以内(包括10吨)的用户,每吨水收费a元,每月用水超过10吨的部分,按每吨b元(b>a)收费,设一户居民月用水x(吨),应收水费y(元),y与x之间的函数关系如图所示.
我国是世界上严重缺水的国家之一,为了增强居民的节水意识,某自来水公司对居民用水采取以户为单位分段计费办法收费:即每月用水10吨以内(包括10吨)的用户,每吨水收费a元,每月用水超过10吨的部分,按每吨b元(b>a)收费,设一户居民月用水x(吨),应收水费y(元),y与x之间的函数关系如图所示.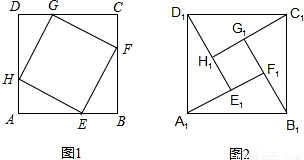 在正方形ABCD中,AB=4cm,点E,F,G,H分别是正方形的四条边上的点,且AE=BF=CG=DH.如图1所示.若把图1中的四个直角三角形剪下来,拼成如图2所示的面积为10cm2的正方形A1B1C1D1,则中间四边形E1F1G1H1的面积等于
在正方形ABCD中,AB=4cm,点E,F,G,H分别是正方形的四条边上的点,且AE=BF=CG=DH.如图1所示.若把图1中的四个直角三角形剪下来,拼成如图2所示的面积为10cm2的正方形A1B1C1D1,则中间四边形E1F1G1H1的面积等于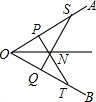 如图,在∠AOB的OA边上取两点P和S,再在OB上取两点Q和T,使OP=OQ,OT=OS,PT=QS,PT与QS相交于点N,求证:ON平分∠AOB.
如图,在∠AOB的OA边上取两点P和S,再在OB上取两点Q和T,使OP=OQ,OT=OS,PT=QS,PT与QS相交于点N,求证:ON平分∠AOB.



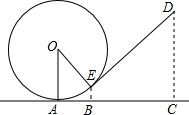 如图是小朋友玩的“滚铁环”游戏的示意图,⊙O向前滚动时,铁棒DE保持与OE垂直.⊙O与地面接触点为A,若⊙O的半径为25cm,cos∠AOE=
如图是小朋友玩的“滚铁环”游戏的示意图,⊙O向前滚动时,铁棒DE保持与OE垂直.⊙O与地面接触点为A,若⊙O的半径为25cm,cos∠AOE= 如图,AB是⊙O的直径,∠C=40°,则∠ABD=
如图,AB是⊙O的直径,∠C=40°,则∠ABD=