题目内容
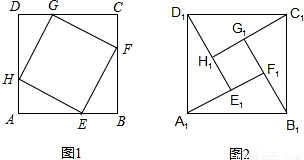 在正方形ABCD中,AB=4cm,点E,F,G,H分别是正方形的四条边上的点,且AE=BF=CG=DH.如图1所示.若把图1中的四个直角三角形剪下来,拼成如图2所示的面积为10cm2的正方形A1B1C1D1,则中间四边形E1F1G1H1的面积等于
在正方形ABCD中,AB=4cm,点E,F,G,H分别是正方形的四条边上的点,且AE=BF=CG=DH.如图1所示.若把图1中的四个直角三角形剪下来,拼成如图2所示的面积为10cm2的正方形A1B1C1D1,则中间四边形E1F1G1H1的面积等于考点:图形的剪拼,正方形的性质
专题:
分析:由已知可得出剪下的4个直角三角形全等,且中间四边形E1F1G1H1为正方形.若设其中一个直角边为x,则另一个直角边为4-x,根据勾股定理可求出斜边,即拼成正方形的边长,又由拼成如图2所示的面积为10cm2的正方形,可求出x,和4-x,从而求出中间四边形E1F1G1H1的边长,即得答案.
解答:解:由已知得:剪下的4个直角三角形全等.且中间四边形E1F1G1H1为正方形.
设其中一个直角边为x,则另一个直角边为4-x,
则斜边即所拼正方形的边长为:
,
所以:x2+(4-x)2=10,
解得:x=3或x=1,
由已知可得:D1E1=3,D1H1-1,
∴H1E1=3-1=2,
所以中间四边形的面积为2×2=4(cm2).
故答案为:4.
设其中一个直角边为x,则另一个直角边为4-x,
则斜边即所拼正方形的边长为:
| x2+(4-x)2 |
所以:x2+(4-x)2=10,
解得:x=3或x=1,
由已知可得:D1E1=3,D1H1-1,
∴H1E1=3-1=2,
所以中间四边形的面积为2×2=4(cm2).
故答案为:4.
点评:此题考查的是勾股定理及正方形的性质,解题的关键是由已知先用直角三角形的直角边表示出所拼正方形的边长,求出两直角边,再求其面积.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案
相关题目
如图的坐标平面上有一正五边形ABCDE,其中C、D两点坐标分别为(1,0)、(2,0).若在没有滑动的情况下,将此正五边形沿着x轴向右滚动,则滚动过程中,下列哪个点会经过点(76,0)?( )
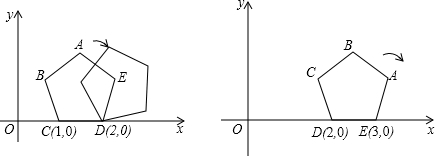

| A、A | B、B | C、C | D、D |
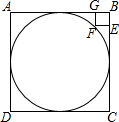 圆与正方形ABCD内切,BEFG为边长1的正方形.求正方形ABCD的边长( )
圆与正方形ABCD内切,BEFG为边长1的正方形.求正方形ABCD的边长( )A、4+2
| ||
| B、2π | ||
C、5
| ||
D、
| ||
E、4
|
在圆外切四边形ABCD中,AB:BC:CD:AD只可能是( )
| A、2:3:4:5 |
| B、3:4:6:5 |
| C、5:4:1:3 |
| D、3:4:2:5 |
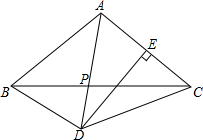 如图,在△ABC中,AB=AC,DE垂直平分AC,且∠CBD=30°,连接BD
如图,在△ABC中,AB=AC,DE垂直平分AC,且∠CBD=30°,连接BD 如图,已知AB⊥BC,AD⊥DE,BC与DE相交于点F,且BC=DE,AC=AE,连接CD、EB.求证:∠CDF=∠EBF.
如图,已知AB⊥BC,AD⊥DE,BC与DE相交于点F,且BC=DE,AC=AE,连接CD、EB.求证:∠CDF=∠EBF. 某中学八年级共有400名学生,学校为了增强学生的环保意识,在本年级进行了一次环保知识测验.为了了解这次测验的成绩状况,学校从中抽取了50名学生的成绩,将所得数据整理后,画出的频数分布直方图如图所示.
某中学八年级共有400名学生,学校为了增强学生的环保意识,在本年级进行了一次环保知识测验.为了了解这次测验的成绩状况,学校从中抽取了50名学生的成绩,将所得数据整理后,画出的频数分布直方图如图所示.