题目内容
如图，AB是⊙O的直径，∠C=40°，则∠ABD=考点：圆周角定理
专题：
分析：首先连接AD，由AB是⊙O的直径，可证∠ADB=90°，由圆周角定理可证∠A=∠C=40°，即可求∠ABD．
解答：
解：连接AD，
∵AB是⊙O的直径，
∴∠ADB=90°，
∵∠A=∠C=40°，
∴∠ABD=90°-∠A=50°．
故答案为：50°．
解：连接AD，∵AB是⊙O的直径，
∴∠ADB=90°，
∵∠A=∠C=40°，
∴∠ABD=90°-∠A=50°．
故答案为：50°．
点评：本题考查了圆周角定理，关键是掌握圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．
推论：半圆（或直径）所对的圆周角是直角，90°的圆周角所对的弦是直径．
推论：半圆（或直径）所对的圆周角是直角，90°的圆周角所对的弦是直径．
练习册系列答案
相关题目
如图，已知AB⊥BC，AD⊥DE，BC与DE相交于点F，且BC=DE，AC=AE，连接CD、EB．求证：∠CDF=∠EBF．
如图，是由7块正方体木块堆成的物体，分别画出从正面、左面、上面看的平面图形．在圆外切四边形ABCD中，AB：BC：CD：AD只可能是（ ）
| A、2：3：4：5 |
| B、3：4：6：5 |
| C、5：4：1：3 |
| D、3：4：2：5 |
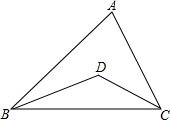如图，BD、CD分别是∠ABC和∠ACB的角平分线，BD、CD相交于点D．
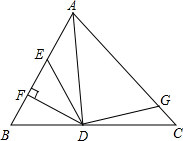如图，AD是△ABC的角平分线，DF⊥AB，垂足为F，DE=DG，△ADG和△AED的面积分别为50和40，则△EDF的面积为