题目内容
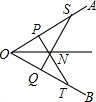 如图,在∠AOB的OA边上取两点P和S,再在OB上取两点Q和T,使OP=OQ,OT=OS,PT=QS,PT与QS相交于点N,求证:ON平分∠AOB.
如图,在∠AOB的OA边上取两点P和S,再在OB上取两点Q和T,使OP=OQ,OT=OS,PT=QS,PT与QS相交于点N,求证:ON平分∠AOB.考点:全等三角形的判定与性质
专题:证明题
分析:证出△SOQ≌△TOP推出∠OSQ=∠PTO,求出PS=TQ,证出△PSN≌△QTN,推出NS=NT,证出△SON≌△TON,推出∠SON=∠TON,即可得出答案.
解答:证明:∵在△SOQ和△TOP中
∴△SOQ≌△TOP(SSS),
∴∠OSQ=∠PTO,
∵OS=OT,OP=OQ,
∴PS=TQ,
在△PSN和△QTN中
∴△PSN≌△QTN(AAS),
∴NS=NT,
在△SON和△TON中
∴△SON≌△TON(SAS),
∴∠SON=∠TON,
即ON平分∠AOB.
|
∴△SOQ≌△TOP(SSS),
∴∠OSQ=∠PTO,
∵OS=OT,OP=OQ,
∴PS=TQ,
在△PSN和△QTN中
|
∴△PSN≌△QTN(AAS),
∴NS=NT,
在△SON和△TON中
|
∴△SON≌△TON(SAS),
∴∠SON=∠TON,
即ON平分∠AOB.
点评:此题考查了全等三角形的判定与性质,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
用平面去截一个几何体,如果截面是圆形,则原几何体可能是( )
| A、正方体、球 |
| B、圆锥、棱柱 |
| C、球、长方体 |
| D、圆柱、圆锥、球 |
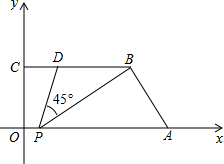 如图,在平面直角坐标系中A(6,0),B(5,3),C(0,3),D(1,3),点P为线段OA上一点且∠BPD=45°,则点P坐标为
如图,在平面直角坐标系中A(6,0),B(5,3),C(0,3),D(1,3),点P为线段OA上一点且∠BPD=45°,则点P坐标为 如图,已知AB⊥BC,AD⊥DE,BC与DE相交于点F,且BC=DE,AC=AE,连接CD、EB.求证:∠CDF=∠EBF.
如图,已知AB⊥BC,AD⊥DE,BC与DE相交于点F,且BC=DE,AC=AE,连接CD、EB.求证:∠CDF=∠EBF. 如图,∠AOB与∠BOC互补,OM平分∠BOC,∠AON=
如图,∠AOB与∠BOC互补,OM平分∠BOC,∠AON=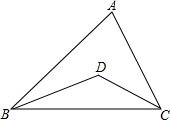 如图,BD、CD分别是∠ABC和∠ACB的角平分线,BD、CD相交于点D.
如图,BD、CD分别是∠ABC和∠ACB的角平分线,BD、CD相交于点D.