题目内容
19．点A（1，a）是抛物线y=$\sqrt{3}$x2上的点，以点A为一个顶点作边长为2的等边△ABC，使点B、C中至少有一个点在这条抛物线上，这样的△ABC共有7个．分析 根据题意画出图象，根据图象即可求得．
解答 
解：如图，因为点A（1，a）是抛物线y=$\sqrt{3}$x2上的点，
所以A（1，$\sqrt{3}$），
所以，OA=2，
以A为圆心，以OA为半径画圆交抛物线四个点，以这四个点和A点构成的线段为边作等边三角形作8个，其中重合一个，故可以作7个，
故答案为7．
点评 本题考查了二次函数图象上点的坐标特征和等边三角形的性质，根据题意作出函数的图象是解题的关键，
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
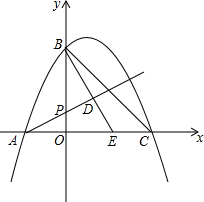已知在平面直角坐标系xOy（如图）中，抛物线y=-x2+bx+c与x轴交于点A（-1，0）与点C（3，0），与y轴交于点B，点P为OB上一点，过点B作射线AP的垂线，垂足为点D，射线BD交x轴于点E．
实数a，b，c，d在数轴上的对应点的位置如图所示，这四个数中，绝对值最大的是a．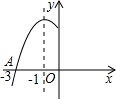
如图，是二次函数y=ax2+bx+c图象的一部分，图象过点A（-3，0），对称轴为x=-1，给出四个结论：
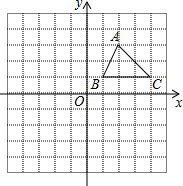如图，已知A（2，3）、B（1，1）、C（4，1）是平面直角坐标系中的三点．
如图是有关x的代数式的方阵，若第10行第2项的值为1034，则此时x的值为2．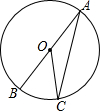
如图，在⊙O中，AB是直径，C是圆上一点，且∠BOC=40°，则∠ACO=20°．